29Exercices corrigés : calcul d'integrale
بسم الله الرحمن الرحيم
I. Détermination de primitives
Exercice 1:
Vérifier que $F$ est une primitive de $f$ sur $I\!R$ avec
1. $f(x)=\displaystyle\frac{1}{1+ e ^{x}}$; $F(x)=x-\ln \left(1+ e ^{x}\right)$
2. $f(x)=\sqrt{e^{x}}$; $F(x)=2 \sqrt{e^{x}}$
Réponse :
1. On dérive $F(x)=x-\ln \left(1+ e ^{x}\right)$
$\begin{aligned} F^{\prime}(x)&=1-\displaystyle\frac{ e ^{x}}{1+ e ^{x}}\\&=\displaystyle\frac{1+ e ^{x}- e ^{x}}{1+ e ^{x}}\\&=\displaystyle\frac{1}{1+ e ^{x}}\\&=f(x) \end{aligned}$
$F$ est donc bien une primitive de $f$ sur $I\!R$
2. On dérive $F(x)=2 \sqrt{ e ^{x}}$
$\begin{aligned} F^{\prime}(x)&=2 \times \displaystyle\frac{e^{x}}{2 \sqrt{ e ^{x}}}\\&=\displaystyle\frac{\sqrt{ e ^{x}}^{2}}{\sqrt{ e ^{x}}}\\&=\sqrt{ e ^{x}}\\&=f(x)\end{aligned}$
$F$ est donc bien une primitive de $f$ sur $I\!R$
Exercice 2: Primitives de sommes de fonctions usuelles
Déterminer une primitive de chacune des fonctions suivantes:
$f_{1}(x)=4 x^{3}+3 x^{2}+2 x+1$ sur $I= I\!R$
$f_{2}(x)=6 x^{5}+4 x^{3}-1$ sur $I= I\!R$
$f_{3}(x)=x^{3}+x^{2}+x+1$ sur $I= I\!R$
$f_{4}(x)=4 x^{7}-x^{6}-\displaystyle\frac{2}{3} x-5$ sur $I= I\!R$
$f_{5}(x)=\displaystyle\frac{1}{2 \sqrt{x}}+9$ sur $I=] 0 ;+\infty[$
$f_{6}(x)=\sin x-3 \cos x$ sur $I= I\!R$
$f_{7}(x)=\displaystyle\frac{2}{x}$ sur $I= I\!R ^{*}$
$f_{8}(x)=-\displaystyle\frac{1}{x^{2}}+\displaystyle\frac{1}{x}- e ^{x}$ sur $I= I\!R ^{*}$
Réponse :
$\bullet \ f_{1}(x)=4 x^{3}+3 x^{2}+2 x+1$ sur $I= I\!R$
$\begin{aligned}F_{1}(x)&=4 \times \displaystyle\frac{x^{4}}{4}+3 \times \displaystyle\frac{x^{3}}{3}+2 \times \displaystyle\frac{x^{2}}{2}+x\\&=x^{4}+x^{3}+x^{2}+x \end{aligned}$
car $F_{1}^{\prime}=f_{1}$
$\bullet \ f_{2}(x)=6 x^{5}+4 x^{3}-1$ sur $I= I\!R$
$\begin{aligned} F_{2}(x)&=6 \times \displaystyle\frac{x^{6}}{6}+4 \times \displaystyle\frac{x^{4}}{4}-x\\&=x^{6}+x^{4}-x \end{aligned}$
car $F_{2}^{\prime}=f_{2}$
$\bullet \ f_{3}(x)=x^{3}+x^{2}+x+1$ sur $I= I\!R$
$F_{3}(x)=\displaystyle\frac{x^{4}}{4}+\displaystyle\frac{x^{3}}{3}+\displaystyle\frac{x^{2}}{2}+x$
car $F_{3}^{\prime}=f_{3}$
$\bullet \ f_{4}(x)=4 x^{7}-x^{6}-\displaystyle\frac{2}{3} x-5$ sur $I= I\!R$
$\begin{aligned} F_{4}(x)&=4 \times \displaystyle\frac{x^{8}}{8}-\displaystyle\frac{x^{7}}{7}-\displaystyle\frac{2}{3} \times \displaystyle\frac{x^{2}}{2}-5 x\\&=\displaystyle\frac{x^{8}}{2}-\displaystyle\frac{x^{7}}{7}-\displaystyle\frac{x^{2}}{3}-5 x \end{aligned}$
car $F_{4}^{\prime}=f_{4}$
$\bullet \ f_{5}(x)=\displaystyle\frac{1}{2 \sqrt{x}}+9$ sur $I=] 0 ;+\infty[$
$F_{5}(x)=\sqrt{x}+9 x$ car $F_{5}^{\prime}=f_{5}$
$\bullet \ f_{6}(x)=\sin x-3 \cos x$ sur $I= I\!R$
$F_{6}(x)=-\cos x-3 \sin x$ car $F_{6}^{\prime}=f_{6}$
$\bullet \ f_{7}(x)=\displaystyle\frac{2}{x}$ sur $I=I\!R ^{*}$
$F_{7}(x)=2 \times \ln |x|$ car $F_{7}^{\prime}=f_{7}$
$\bullet \ f_{8}(x)=-\displaystyle\frac{1}{x^{2}}+\displaystyle\frac{1}{x}- e ^{x}$ sur $I=I\!R ^{*}$
$F_{8}(x)=\displaystyle\frac{1}{x}+\ln |x|- e ^{x}$ car $F_{8}^{\prime}=f_{8}$
Exercice3:
Primitives de $\displaystyle\frac{u^{\prime}}{u}, \displaystyle\frac{u^{\prime}}{u^{2}}$ et $u^{\prime} e ^{u}$
Déterminer une primitive de chacune des fonctions suivantes:
$f_{1}(x)=\displaystyle\frac{2 x}{x^{2}+1}$ sur $I= I\!R$
$f_{2}(x)=\displaystyle\frac{4 x^{3}}{\left(x^{4}+1\right)^{2}}$ sur $I= I\!R$
$f_{3}(x)=3 x e ^{3 x^{2}+1}$ sur $I= I\!R$
$f_{4}(x)=\displaystyle\frac{ e ^{x}}{\left( e ^{x}+1\right)^{2}}$ sur $I= I\!R$
$f_{5}(x)=\displaystyle\frac{ e ^{x}}{ e ^{x}+3}$ sur $I= I\!R$
$f_{6}(x)=\cos x e ^{\sin x}$ sur $I= I\!R$
Réponse :
Primitives de $\displaystyle\frac{u^{\prime}}{u}$, $\displaystyle\frac{u^{\prime}}{u^{2}}$ et $u^{\prime} e ^{u}$
$\bullet \ f_{1}(x)=\displaystyle\frac{2 x}{x^{2}+1}$ sur $I=I\!R$ :
$f_{1}$ est de la forme $\displaystyle\frac{u^{\prime}}{u}$ avec $u(x)=x^{2}+1>0$
Une primitive de $f_{1}$ est donc $F_{1}(x)=\ln u(x)=\ln \left(x^{2}+1\right)$ sur $I\!R$
$\bullet \ f_{2}(x)=\displaystyle\frac{4 x^{3}}{\left(x^{4}+1\right)^{2}}$ sur $I=I\!R$ :
$f_{2}$ est de la forme $\displaystyle\frac{u^{\prime}}{u^{2}}$ avec $u(x)=x^{4}+1>0$
Une primitive de $f_{2}$ est donc $F_{2}(x)=-\displaystyle\frac{1}{u(x)}=-\displaystyle\frac{1}{x^{4}+1}$ sur $I\!R$
$\bullet \ f_{3}(x)=3 x e ^{3 x^{2}+1}=\displaystyle\frac{1}{2} \times 6 x e ^{3 x^{2}+1}$ sur $I=I\!R$ :
$f_{3}$ est de la forme $\displaystyle\frac{1}{2} u^{\prime} e ^{u}$ avec $u(x)=3 x^{2}+1$
Une primitive de $f_{3}$ est donc $F_{3}(x)=\displaystyle\frac{1}{2} e ^{u(x)}=\displaystyle\frac{ e ^{3 x^{2}-1}}{2}$ sur $I\!R$
$\bullet \ f_{4}(x)=\displaystyle\frac{ e ^{x}}{\left( e ^{x}+1\right)^{2}}$ sur $I=I\!R$ :
$f_{4}$ est de la forme $\displaystyle\frac{u^{\prime}}{u^{2}}$ avec $u(x)= e ^{x}+1$
Une primitive de $f_{4}$ est donc $F_{4}(x)=-\displaystyle\frac{1}{u(x)}=-\displaystyle\frac{1}{ e ^{x}+1}$ sur $I\!R$
$\bullet \ f_{5}(x)=\displaystyle\frac{ e ^{x}}{ e ^{x}+3} \quad$ sur $I=I\!R$ :
$f_{5}$ est de la forme $\displaystyle\frac{u^{\prime}}{u}$ avec $u(x)= e ^{x}+3$
Une primitive de $f_{5}$ est donc $F_{5}(x)=\ln |u(x)|=\ln \left( e ^{x}+3\right)$ car $e ^{x}+3>0$ sur $I\!R$
$\bullet\ f_{6}(x)=\cos x e ^{\sin x}$ sur $I=I\!R$ :
$f_{6}$ est de la forme $u$ 'e $^{u}$ avec $u(x)=\sin x$
Une primitive de $f_{6}$ est donc $F_{6}(x)= e ^{u(x)}= e ^{\sin x}$ sur $I\!R$
Exercice4:
Déterminer toutes les primitives sur $I\!R$ de la fonction $f$ , définie sur $I\!R$ par $f(x)=\displaystyle\frac{x}{x^{2}+4}$
Réponse :
On a $f(x)=\displaystyle\frac{x}{x^{2}+4}=\displaystyle\frac{1}{2} \times \displaystyle\frac{2 x}{x^{2}+4}$ .
La fonction est de la forme $\displaystyle\frac{1}{2} \times\displaystyle\frac{u^{\prime}}{u}$ avec $u(x)=x^{2}+4$
Les primitives de $f$ sur $I\!R$, sont donc de la forme $F(x)=\displaystyle\frac{1}{2} \ln \left(x^{2}+4\right)+C$, $C \in I\!R$
Exercice 5 :
Déterminez une primitive de la fonction $f$ proposée sur l'intervalle $I$ donné :
1) $f(x)=\frac{1}{4} e^{x}$ sur $I\!R$
2) $f(x)=e^{-x}$ sur $I\!R$
3) $f(x)=e^{2 x+3}$ sur $I\!R$
4) $f(x)=x e^{x^{2}}$ sur $I\!R$
5) $f(x)=\frac{e^{x}}{e^{x}+1}$ sur $I\!R$
Réponse :
1) $f(x)=\frac{1}{4} e^{x}$
$f$ est définie et continue sur $I\!R$ en tant que produit de fonctions qui le sont, donc admet des primitives sur $I\!R$, et pour tout $F(x)=\frac{1}{4} e^{x}$.
2) $f(x)=e^{-x}$
$f$ est définie et continue sur $I\!R$ en tant que composée de fonctions qui le sont, donc admet des primitives sur $I\!R$, et puisque pour tout $x \in I\!R$,
$f(x)=-\left(-e^{-x}\right)=-u^{\prime}(x) e^{u(x)}$ ou $u(x)=-x \Rightarrow u^{\prime}(x)=-1$,
$F(x)=e^{u(x)}=e^{-x}$
3) $f(x)=e^{2 x+3}$
$f$ est définie et continue sur $I\!R$ en tant que composée de fonctions qui le sont, donc admet des primitives sur $I\!R$, et puisque pour tout $x \in I\!R$, $f(x)=\frac{1}{2} \times 2 e^{2 x+3}=\frac{1}{2} u^{\prime}(x) e^{u(x)}$ ou $u(x)=2 x+3 \Rightarrow u^{\prime}(x)=2$,
$F(x)=\frac{1}{2} e^{u(x)}=\frac{1}{2} e^{2 x+3}$
4) $f(x)=x e^{x^{2}}$
$f$ est définie et continue sur $I\!R$ en tant que produit de fonctions qui le sont, donc admet des primitives sur $I\!R$, et puisque pour tout $x \in I\!R$, $f(x)=\frac{1}{2} \times 2 x e^{x^{2}}=\frac{1}{2} u^{\prime}(x) e^{u(x)}$ ou $u(x)=x^{2} \Rightarrow u^{\prime}(x)=2 x$,
$F(x)=\frac{1}{2} e^{u(x)}=e^{x^{2}}$
5) $f(x)=\frac{e^{x}}{e^{x}+1}$
$f$ est définie et continue sur $I\!R$ en tant que quotient de fonctions qui le sont, le dénominateur ne s'annulant pas (car $x \in I\!R \Rightarrow e^{x}+1>0$ donc $\neq 0$ ) donc admet des primitives sur $I\!R$, et puisque pour tout $x \in I\!R$ $f(x)=\frac{u^{\prime}(x)}{u(x)}$ ou $u(x)=e^{x} \Rightarrow u^{\prime}(x)=e^{x}$,
$\begin{aligned}F(x)&=\ln (|u(x)|)\\&=\ln \left(\left|e^{x}+1\right|\right)\\&=\ln \left(e^{x}+1\right)\end{aligned}$
car $x \in I\!R \Rightarrow e^{x}+1>0$
Exercice 6 :
Soit $f$ la fonction définie sur IR par $f(x)=(x+2) e^{x}$
Déterminez les nombres $a$ et $b$ tels que la fonction $F$, définie sur IR, par $F(x)=(a x+b) e^{x}$ soit une primitive de $f$.
RÉPONSE :
La fonction $F$, définie sur $I\!R$, par $F(x)=(a x+b) e^{x}$ est dérivable sur $I\!R$ en tant que produit de fonction qui le sont, et pour tout $x \in I\!R$, $F^{\prime}(x)=a e^{x}+(a x+b) e^{x}=(a x+a+b) e^{x}$
$F$ sera une primitive de $f$ si et seulement si pour tout $x \in I\!R$,
$F^{\prime}(x)=f(x) \Leftrightarrow\left\{\begin{array}{l}a=1 \\ a+b=2\end{array}\right.$
Une primitive de $f$ sur $I\!R$ est donc $F(x)=(x+1) e^{x}$
Exercice 7 :
1) Déterminer la primitive sur $I\!R$ de la fonction cosinus qui s'annule en $\displaystyle\frac{\pi}{2}$
2) Déterminer la primitive de la fonction $f$, définie sur $I\!R$ par $f(x)= e ^{3 x+1}$, qui s'annule en $x=-1$
3) Déterminer la primitive de la fonction $f$, définie sur $I\!R$ par $f(x)=x e ^{-x^{2}},$ dont la courbe représentative passe par le point $A(\sqrt{\ln 2}, 1)$
Réponse :
1) Les primitives de la fonction cosinus sont de la forme $F(x)=\sin x+C$, $C \in I\!R .$
On cherche alors $C$ tel que $F(\displaystyle\frac{\pi}{2})=0 .$
On a $F(\displaystyle\frac{\pi}{2})=\sin \displaystyle\frac{\pi}{2}+C=1+C$
Il faut donc que $C=-1$ et la primitive cherchée est $F(x)=\sin x-1$
2) On a $f(x)=\displaystyle\frac{1}{3} \times 3 e ^{3 x+1}$ .
La fonction est de la forme $\displaystyle\frac{1}{3} \times u'e^{u}$ avec $u(x)=3 x+1$
Les primitives de la fonction $f$ sont donc de la forme $F(x)= e ^{3 x+1}+C$, $C \in I\!R$
On cherche alors $C$ tel que $F(-1)=0$ .
On a
$\begin{aligned}F(-1)&= e ^{3 \times(-1)+1}+C\\&= e ^{-2}+C\\&=\displaystyle\frac{1}{ e ^{2}}+C\end{aligned}$
Il faut donc que $C=-\displaystyle\frac{1}{ e ^{2}}$ et la primitive cherchée est $F(x)= e ^{3 x+1}-\displaystyle\frac{1}{ e^{2}}$
3) On a $f(x)=-\displaystyle\frac{1}{2} \times(-2 x) e ^{-x^{2}}$ .
La fonction est de la forme $-\displaystyle\frac{1}{2} \times u^{\prime} e ^{u}$ avec $u(x)=-x^{2}$
Les primitives de la fonction $f$ sont donc de la forme $F(x)=-\displaystyle\frac{1}{2} e ^{-x^{2}}+C$, $C \in I\!R$
On cherche alors $C$ tel que $F(\sqrt{\ln 2})=1$
On a
$\begin{array}{ll}F(\sqrt{\ln 2})&=-\displaystyle\frac{1}{2} e ^{-\sqrt{\ln 2}^{2}}+C\\&=-\displaystyle\frac{1}{2} e ^{-\ln 2}+C\\&=-\displaystyle\frac{1}{2 e ^{\ln 2}}+C\\&=-\displaystyle\frac{1}{4}+C=1\end{array}$
Il faut donc que $C=\displaystyle\frac{5}{4}$ et la primitive cherchée est $F(x)=-\displaystyle\frac{1}{2} e ^{-x^{2}}+\displaystyle\frac{5}{4}$
Exercice 8 :
Soit $f$ la fonction définie sur $I\!R$ par $f(x)=\frac{3}{e^{-x}+1}$
1) Vérifiez que pour tout $x$ de $I\!R$, on a $f(x)=\frac{3 e^{x}}{e^{x}+1}$
2) Déduisez en la primitive $F$ de $f$ qui s'annule pour $x=0$
Réponse :
1) Pour tout $x \in I\!R$,
$\begin{aligned}f(x)&=\frac{3}{e^{-x}+1}\\&=\frac{3 \times e^{x}}{\left(e^{-x}+1\right) \times e^{x}}\\&=\frac{3 e^{x}}{e^{-x} \times e^{x}+1 \times e^{x}}\\&=\frac{3 e^{x}}{1+e^{x}}\end{aligned}$
2) . $f$ est définie et continue sur $I\!R$ en tant que quotient de fonctions qui le sont, le dénominateur ne s'annulant pas (car $x \in I\!R \Rightarrow 1+e^{x}>0$ donc $\neq 0$ ) donc admet des primitives sur $I\!R$, et en utilisant l'écriture $f(x)=\frac{3 e^{x}}{e^{x}+1}=3 \frac{u^{\prime}(x)}{u(x)}$ ou $u(x)=e^{x}+1$,
on obtient
$\begin{aligned}F(x)&=3 \ln (|u(x)|)+k\\&=3 \ln \left(\left|e^{x}+1\right|\right)+k\\&=3 \ln \left(e^{x}+1\right)+k\end{aligned}$
car $e^{x}+1>0$ sur $I\!R$
Exercice 9 :
On considère la fonction $f$ définie sur $] 2 ;+\infty[$ par $f(x)=\displaystyle\frac{2 x^{2}-3 x-4}{x-2}$.
a) Écrire $f$ sous la forme $f(x)=a x+b+\displaystyle\frac{c}{x-2}$
b) Déterminer alors une primitive de $f$
Réponse :
$f$ est la fonction définie sur $] 2 ;+\infty[$ par $f(x)=\displaystyle\frac{2 x^{2}-3 x-4}{x-2}$.
a)
$ \begin{array}{ll} a x+b+\displaystyle\frac{c}{x-2}&=\displaystyle\frac{(a x+b)(x-2)+c}{x-2}\\&=\displaystyle\frac{a x^{2}-2 a x+b x-2 b+c}{x-2}\\&=\displaystyle\frac{a x^{2}+(b-2 a) x+c-2 b}{x-2} \end{array}$
Pour que ce quotient soit égal à $f(x)$, il suffit que :
$\left\{\begin{array}{l}a=2 \\ b-2 a=-3 \\ c-2 b=-4\end{array} \Leftrightarrow\left\{\begin{array}{l}a=2 \\ b=-3+2 \times 2=1 \\ c=-4+2 \times 1=-2\end{array}\right.\right.$
On en déduit que $f(x)=2 x+1-\displaystyle\frac{2}{x-2}$
b) Comme
$\begin{aligned}f(x)&=2 x+1-\displaystyle\frac{2}{x-2}\\&=2 x+1-2 \times \displaystyle\frac{1}{x-2}\end{aligned}$,
une primitive de $f$ sur $] 2 ;+\infty[$ est $F(x)=x^{2}+x-2 \ln (x-2)$
II. Calcul d’intégrales à l’aide des primitives :
Exercice 10 :
Calculer les intégrales suivantes:
a) $\displaystyle\int_{-1}^{1}\left(t^{2}+4 t+3\right) dt$
b) $\displaystyle\int_{1}^{2}\left(\displaystyle\frac{1}{2 t}-\displaystyle\frac{3}{t^{2}}\right) dt$
c) $\displaystyle\int_{\ln 2}^{\ln 3} e ^{x} dx$
d) $\displaystyle\int_{1}^{2} \sqrt{t} dt$
e) $\displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}(\cos x-\sin x) dx$
f) $\displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \displaystyle\frac{ dx}{\cos ^{2} x}$
Réponse :
$\begin{array}{ll} a)\ \displaystyle\int_{-1}^{1}\left(t^{2}+4 t+3\right) dt&=\left[\displaystyle\frac{t^{3}}{3}+4 \times \displaystyle\frac{t^{2}}{2}+3 t\right]_{-1}^{1}\\&=\left[\displaystyle\frac{t^{3}}{3}+2 t^{2}+3 t\right]_{-1}^{1}\\&=\left(\displaystyle\frac{1}{3}+2+3\right)-\left(\displaystyle\frac{-1}{3}+2-3\right)\\&=\displaystyle\frac{20}{3} \end{array}$
$\begin{array}{ll}b)\ \displaystyle\int_{1}^{2}\left(\displaystyle\frac{1}{2 t}-\displaystyle\frac{3}{t^{2}}\right) dt&=\displaystyle\int_{1}^{2}\left(\displaystyle\frac{1}{2} \times \displaystyle\frac{1}{t}+3 \times\left(-\displaystyle\frac{1}{t^{2}}\right)\right) dt\\&=\left[\displaystyle\frac{1}{2} \ln t+3 \times \displaystyle\frac{1}{t}\right]_{1}^{2}\\&=\displaystyle\frac{1}{2} \ln 2+\displaystyle\frac{3}{2}-\left(\displaystyle\frac{1}{2} \ln 1+3\right)\\&=\displaystyle\frac{1}{2} \ln 2-\displaystyle\frac{3}{2}\end{array}$
$ c)\ \displaystyle\int_{\ln 2}^{\ln 3} e ^{x} dx=\left[ e ^{x}\right]_{\ln 2}^{\ln 3}= e ^{\ln 3}- e ^{\ln 2}=1$
$\begin{array}{ll}d)\ \displaystyle\int_{1}^{2} \sqrt{t} dt&=\displaystyle\int_{1}^{2} t^{\frac{1}{2}} dt\\&=\left[\displaystyle\frac{t^{\frac{3}{2}}}{\frac{3}{2}}\right]_{1}^{2}\\&=\left[\displaystyle\frac{2}{3} t^{\frac{3}{2}}\right]_{1}^{2}\\&=\displaystyle\frac{2}{3}\left(2^{\frac{3}{2}}-1\right)\\&=\displaystyle\frac{2}{3}(2 \sqrt{2}-1) \end{array}$
$\begin{array}{ll}e)\ \displaystyle\int_{\frac{\pi}{6}}^{\frac{\pi}{2}}(\cos x-\sin x) dx&=[\sin x+\cos x]_{\frac{\pi}{6}}^{\frac{\pi}{2}}\\&=\left(\sin \displaystyle\frac{\pi}{2}+\cos \displaystyle\frac{\pi}{2}\right)-\left(\sin \displaystyle\frac{\pi}{6}+\cos \displaystyle\frac{\pi}{6}\right)\\&=1-\left(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}\right)\\&=\displaystyle\frac{1-\sqrt{3}}{2}\end{array}$
$f)\ \displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} \displaystyle\frac{ dx}{\cos ^{2} x}=[\tan x]_{\frac{\pi}{4}}^{\frac{\pi}{3}}=\sqrt{3}-1$
Exercice 11 :
Calculer les intégrales suivantes:
a) $\displaystyle\int_{0}^{\ln 3} e ^{-t} dt$
b) $\displaystyle\int_{0}^{2} \displaystyle\frac{x}{\left(x^{2}+1\right)^{2}} dx$
c) $\displaystyle\int_{0}^{-1} \displaystyle\frac{ dt}{\sqrt{1-2 t}}$
d) $\displaystyle\int_{1}^{2} \displaystyle\frac{dx}{3 x+2}$
e) $\displaystyle\int_{\frac{1}{ e }}^{ e } \displaystyle\frac{\ln t}{t} dt$
f) $\displaystyle\int_{0}^{1} \sqrt{2-t} dt$
g) $\displaystyle\int_{0}^{\ln 2} \displaystyle\frac{e^{2 t}}{e^{2 t}+1} dt$
h) $\displaystyle\int_{0}^{\frac{\pi}{2}} \sin (2 t) dt$
i) $\displaystyle\int_{\frac{\pi}{2}}^{\frac{3 \pi}{4}} \cos (3 x) dx$
Réponse :
$\begin{array}{ll} a)\ \displaystyle\int_{0}^{\ln 3} e ^{-t} dt&=\left[- e ^{-t}\right]_{0}^{\ln 3}\\&=- e ^{-\ln 3}-\left(- e ^{0}\right)\\&=-\displaystyle\frac{1}{3}+1\\&=\displaystyle\frac{2}{3}\end{array}$
Pour toute la suite, on note $f$ la fonction à intégrer, $F$ une primitive de $f$ et $I$ l'intégrale à calculer.
$b)\ \displaystyle\int_{0}^{2} \displaystyle\frac{x}{\left(x^{2}+1\right)^{2}} dx:$
soit $u(x)=x^{2}+1 ;$ alors $u^{\prime}(x)=2 x$
$\begin{aligned}f(x)&=\displaystyle\frac{x}{\left(x^{2}+1\right)^{2}}\\&=\displaystyle\frac{1}{2} \times \displaystyle\frac{2 x}{\left(x^{2}+1\right)^{2}}\\&=\displaystyle\frac{1}{2} \times \displaystyle\frac{u^{\prime}(x)}{(u(x))^{2}}\end{aligned}$
donc
$\begin{aligned}F(x)&=\displaystyle\frac{1}{2} \times\left(-\displaystyle\frac{1}{u(x)}\right)\\&=-\displaystyle\frac{1}{2\left(x^{2}+1\right)}\end{aligned}$
$\begin{aligned}I&=\left[-\displaystyle\frac{1}{2\left(x^{2}+1\right)}\right]_{0}^{2}\\&=-\displaystyle\frac{1}{10}-\left(-\displaystyle\frac{1}{2}\right)\\&=\displaystyle\frac{2}{5}\end{aligned}$
$c)\ \displaystyle\int_{0}^{-1} \displaystyle\frac{ dt}{\sqrt{1-2 t}}$:
soit $u(t)=1-2 t$ ; alors $u^{\prime}(t)=-2$
$\begin{aligned}f(t)&=\displaystyle\frac{1}{\sqrt{1-2 t}}\\&=-\displaystyle\frac{1}{2} \times \displaystyle\frac{-2}{\sqrt{1-2 t}}\\&=-\displaystyle\frac{u^{\prime}(t)}{2 \sqrt{u(t)}}\end{aligned}$
donc
$F(t)=-\sqrt{u(t)}=-\sqrt{1-2 t}$
$\begin{aligned}I&=[-\sqrt{1-2 t}]_{0}^{-1}\\&=-\sqrt{3}-(-1)\\&=1-\sqrt{3}\end{aligned}$
$d)\ \displaystyle\int_{1}^{2} \displaystyle\frac{dx}{3 x+2}:$
soit $u(x)=3 x+2 ;$ alors $u^{\prime}(x)=3$
$\begin{aligned}f(x)&=\displaystyle\frac{1}{3 x+2}\\&=\displaystyle\frac{1}{3} \times \displaystyle\frac{3}{3 x+2}\\&=\displaystyle\frac{1}{3} \times \displaystyle\frac{u^{\prime}(x)}{u(x)}\end{aligned}$
donc
$\begin{aligned}F(x)&=\displaystyle\frac{1}{3} \ln (u(x))\\&=\displaystyle\frac{1}{3} \ln (3 x+2)\end{aligned}$
$\begin{aligned}I&=\left[\displaystyle\frac{1}{3} \ln (3 x+2)\right]_{1}^{2}\\&=\displaystyle\frac{1}{3}(\ln 8-\ln 5)\\&=\displaystyle\frac{1}{3} \ln \displaystyle\frac{8}{5}\end{aligned}$
$e)\ \displaystyle\int_{\frac{1}{ e }}^{ e } \displaystyle\frac{\ln t}{t} dt:$
soit $u(t)=\ln t ;$ alors $u^{\prime}(t)=\displaystyle\frac{1}{t}$
$\begin{aligned}f(t)=\displaystyle\frac{\ln t}{t}&=\ln t \times \displaystyle\frac{1}{t}\\&=u(t) \times u^{\prime}(t)\end{aligned}$
donc
$\begin{aligned}F(t)&=\displaystyle\frac{(u(t))^{2}}{2}\\&=\displaystyle\frac{(\ln t)^{2}}{2}\end{aligned}$
$\begin{aligned}I&=\left[\displaystyle\frac{(\ln t)^{2}}{2}\right]_{\frac{1}{ e }}^{ e }\\&=\displaystyle\frac{1}{2}\left((\ln e )^{2}-\left(\ln \displaystyle\frac{1}{ e }\right)^{2}\right)\\&=0\end{aligned}$
$f)\ \displaystyle\int_{0}^{1} \sqrt{2-t} dt:$
soit $u(t)=2-t ;$ alors $u^{\prime}(t)=-1$
$f(t)=\sqrt{2-t}=(2-t)^{\frac{1}{2}}=-(u(t))^{\frac{1}{2}} \times u^{\prime}(t)$
donc
$\begin{aligned}F(t)&=-\displaystyle\frac{2}{3}(u(t))^{\frac{3}{2}}\\&=-\displaystyle\frac{2}{3}(2-t)^{\frac{3}{2}}\end{aligned}$
$\begin{aligned}I&=\left[-\displaystyle\frac{2}{3}(2-t)^{\frac{3}{2}}\right]_{0}^{1}\\&=-\displaystyle\frac{2}{3}-\left(-\displaystyle\frac{2}{3} \times 2^{\frac{3}{2}}\right)\\&=\displaystyle\frac{2}{3}(2 \sqrt{2}-1) \end{aligned}$
$g)\ \displaystyle\int_{0}^{\ln 2} \displaystyle\frac{e^{2 t}}{e^{2 t}+1} dt:$
soit $u(t)=e^{2 t}+1 ;$ alors $u^{\prime}(t)=2 e^{2 t}$
$\begin{aligned}f(t)&=\displaystyle\frac{ e ^{2 t}}{ e ^{2 t}+1}\\&=\displaystyle\frac{1}{2} \times \displaystyle\frac{2 e ^{2 t}}{ e ^{2 t}+1}\\&=\displaystyle\frac{1}{2} \times \displaystyle\frac{u^{\prime}(t)}{u(t)} \end{aligned}$
donc
$F(t)=\displaystyle\frac{1}{2} \ln (u(t))=\displaystyle\frac{1}{2} \ln \left(e^{2 t}+1\right)$
$\begin{aligned}I&=\left[\displaystyle\frac{1}{2} \ln \left( e ^{2 t}+1\right)\right]_{0}^{\ln 2}\\&=\displaystyle\frac{1}{2}\left(\ln \left( e ^{2 \ln 2}+1\right)-\ln \left( e ^{0}+1\right)\right)\\&=\displaystyle\frac{1}{2} \ln \displaystyle\frac{5}{2}\end{aligned}$
$h)\ \displaystyle\int_{0}^{\frac{\pi}{2}} \sin (2 t) dt:$
soit $u(t)=2 t ;$ alors $u^{\prime}(t)=2$
$\begin{aligned}f(t)&=\sin (2 t)\\&=-\displaystyle\frac{1}{2} \times(-\sin (2 t)) \times 2\\&=-\displaystyle\frac{1}{2} \times(\cos )^{\prime}(u(t)) \times u^{\prime}(t) \end{aligned}$
donc
$\begin{aligned}F(t)&=-\displaystyle\frac{1}{2} \cos (u(t))\\&=-\displaystyle\frac{1}{2} \cos (2 t) \end{aligned}$
$\begin{aligned}I&=\left[-\displaystyle\frac{1}{2} \cos (2 t)\right]_{0}^{\frac{\pi}{2}}\\&=-\displaystyle\frac{1}{2} \cos \pi-\left(-\displaystyle\frac{1}{2} \cos 0\right)\\&=1\end{aligned}$
$i)\ \displaystyle\int_{\frac{\pi}{2}}^{\frac{3 \pi}{4}} \cos (3 x) dx:$
soit $u(x)=3 x$ ; alors $u^{\prime}(x)=3$
$\begin{aligned}f(x)&=\cos (3 x)\\&=\displaystyle\frac{1}{3} \times \cos (3 x) \times 3\\&=\displaystyle\frac{1}{3} \times(\sin )^{\prime}(u(x)) \times u^{\prime}(x)\end{aligned}$
donc
$F(x)=\displaystyle\frac{1}{3} \sin (u(x))=\displaystyle\frac{1}{3} \sin (3 x)$
$\begin{array}{ll} I&=\left[\displaystyle\frac{1}{3} \sin (3x)\right]_{\frac{\pi}{2}}^{\frac{3 \pi}{4}}\\&=\displaystyle\frac{1}{3}\left(\sin \displaystyle\frac{9 \pi}{4}-\sin \displaystyle\frac{3 \pi}{2}\right)\\&=\displaystyle\frac{1}{3}\left(\displaystyle\frac{\sqrt{2}}{2}-(-1)\right)\\&=\displaystyle\frac{\sqrt{2}+2}{6} \end{array}$
Exercice 12 :
Calculez les intégrales suivantes:
1) $\int_{2}^{5} e^{x} d x$
2) $\int_{2}^{5}-e^{-x} d x$
3) $\int_{0}^{2} 2 e^{2 x-1} d x$
4) $\int_{2}^{1}\left(e^{2 t}+2 e^{t}-3\right) d t$
5) $\int_{-1}^{1} e^{3 x+1} d x$
6) $\int_{0}^{1} \frac{e^{x}}{e^{x}+1} d x$
7) $\int_{\ln 3}^{\ln 10} e^{x}\left(e^{x}-3\right) d x$
8) $\int_{0}^{1} \frac{e^{-x}-2}{e^{x}} d x$
Réponse :
$\begin{aligned}1)\ \int_{0}^{5} e^{x} d x&=\left[e^{x}\right]_{2}^{5}\\&=e^{5}-e^{2}\end{aligned}$
$\begin{aligned}2)\ \int_{2}^{5}-e^{-x} d x&=\int_{2}^{5} u^{\prime}(x) e^{u(x)} d x\\&=\left[e^{u(x)}\right]_{2}^{5}\\&=\left[e^{-x}\right]_{2}^{5}\\&=e^{-5}-e^{-2}\\&=\frac{1}{e^{5}}-\frac{1}{e^{2}}\\&=\frac{e^{2}-e^{5}}{e^{7}}\end{aligned}$
$\begin{aligned}3)\ \int_{0}^{2} 2 e^{2 x-1} d x&=\int_{0}^{2} u^{\prime}(x) e^{u(x)} d x\\&=\left[e^{u(x)}\right]_{0}^{2}\\&=\left[e^{2 x-1}\right]_{0}^{2}\\&=e^{3}-e^{-1}\\&=e^{3}-\frac{1}{e}\\&=\frac{e^{4}-1}{e} \end{aligned}$
$\begin{aligned}4)\ \int_{2}^{1}\left(e^{2 t}+2 e^{t}-3\right) d t&=\left[\frac{1}{2} e^{2 t}+2 e^{t}-3 t\right]_{2}^{1}\\&=\left(\frac{1}{2} e^{2}+2 e^{1}-3\right)-\left(\frac{1}{2} e^{4}+2 e^{2}-6\right)\\&=-\frac{1}{2} e^{4}+\frac{5}{2} e^{2}+2 e+3 \end{aligned}$
5) $\int_{1}^{1} e^{3 x+1} d x=F(1)-F(-1)$ où $F$ est une primitive de $f(x)=e^{3 x+1}=\frac{1}{3} u^{\prime}(x) e^{u(x)}$, donc $F(x)=\frac{1}{3} e^{u(x)}=\frac{1}{3} e^{3 x+1}$.
Ainsi
$\begin{aligned}\int_{-1}^{1} e^{3 x+1} d x&=\frac{1}{3} e^{3 x \mid+1}-\frac{1}{3} e^{3 \times(-1)+1}\\&=\frac{1}{3}\left(e^{4}-e^{-2}\right)\\&=\frac{1}{3}\left(e^{4}-\frac{1}{e^{2}}\right)\\&=\frac{e^{6}-1}{3 e^{2}}\end{aligned}$
$\begin{aligned}6)\ \int_{0}^{1} \frac{e^{x}}{e^{x}+1} d x&=\int_{0}^{1} \frac{u^{\prime}(x)}{u(x)} d x\\&=[\ln (|u(x)|)]_{0}^{1}\\&=\left[\ln \left(\left|e^{x}+1\right|\right)\right]_{0}^{1}\\&=\left[\ln \left(e^{x}+1\right)\right]_{0}^{1}\\&=\ln (e+1)-\ln (2)\\&=\ln \left(\frac{e+1}{2}\right) \end{aligned}$
$\begin{aligned}7)\ \int_{\ln 3}^{\ln 10} e^{x}\left(e^{x}-3\right) d x&=\int_{1}^{e} u^{\prime}(x) u(x) d x\\&=\left[\frac{u^{2}(x)}{2}\right]_{\ln 3}^{\ln 10}\\&=\left[\frac{\left(e^{x}-3\right)^{2}}{2}\right]_{\ln 3}^{\ln 10}\\&=\frac{\left(e^{\ln 10}-3\right)^{2}}{2}-\frac{\left(e^{\ln 3}-3\right)^{2}}{2}\\&=\frac{(10-3)^{2}}{2}=\frac{49}{2}\end{aligned}$
$\begin{aligned}8)\ \int_{0}^{1} \frac{e^{-x}-2}{e^{x}} d x&=\int_{0}^{1} e^{-x}\left(e^{-x}-2\right) d x\\&=\int_{0}^{1}-u^{\prime}(x) u(x) d x\\&=-\left[\frac{u(x)^{2}}{2}\right]_{0}^{1}\\&=-\left[\frac{\left(e^{-x}-2\right)^{2}}{2}\right]_{0}^{1}\\&-\frac{\left(e^{-1}-2\right)^{2}}{2}+\frac{\left(e^{0}-2\right)^{2}}{2}\\&=-\frac{\left(e^{-1}-2\right)^{2}}{2}+\frac{1}{2} \end{aligned}$
Exercice 13 :
Calculez l'intégrale $I=\int_{0}^{1} \frac{1}{e^{x}+1} d x$ (indication : $\frac{1}{e^{x}+1}=1-\frac{e^{x}}{e^{x}+1}$ )
Exercice 14 :
Soit $f$ la fonction définie sur $]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[$ par: $f(x)=\displaystyle\frac{8 x^{2}-4}{4 x^{2}-1}.$
1) Déterminer les réels $a$, $b$ et $c$ tels que :
pour tout $x \in]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[$, $f(x)=a+\displaystyle\frac{b}{2 x+1}+\displaystyle\frac{c}{2 x-1}.$
2) Calculer l'intégrale $\displaystyle\int_{0}^{\frac{1}{4}} f(x) dx$
Réponse :
$f$ est la fonction définie sur $]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[$ par : $f(x)=\displaystyle\frac{8 x^{2}-4}{4 x^{2}-1}.$
1) $\forall x \in]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[$, $f(x)=a+\displaystyle\frac{b}{2 x+1}+\displaystyle\frac{c}{2 x-1}$
$\Leftrightarrow \forall x \in]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[, f(x)=\displaystyle\frac{a\left(4 x^{2}-1\right)+b(2 x-1)+c(2 x+1)}{(2 x+1)(2 x-1)}$
$\Leftrightarrow \forall x \in]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[, \displaystyle\frac{8 x^{2}-4}{4 x^{2}-1}=\displaystyle\frac{4 a x^{2}+(2 b+2 c) x-a-b+c}{(2 x+1)(2 x-1)}$
$\Leftrightarrow \forall x \in]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}[, 8 x^{2}-4=4 a x^{2}+(2 b+2 c) x-a-b+c $
Deux polynômes sont égaux si et seulement si ils ont le même degré et les mêmes coefficients.
L'égalité précédente équivaut à :
$\left\{\begin{array}{l}4 a=8 \\ 2 b+2 c=0 \\ -a-b+c=-4\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}a=2 \\ c=-b \\ -2-2 b=-4\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}a=2 \\ b=1 \\ c=-1\end{array}\right.$
D'où :pour tout $x \in\left]-\displaystyle\frac{1}{2} ; \displaystyle\frac{1}{2}\right[$, $f(x)=2+\displaystyle\frac{1}{2 x+1}-\displaystyle\frac{1}{2 x-1}$
2) $f(x)=2+\displaystyle\frac{1}{2} \times \displaystyle\frac{2}{2 x+1} \displaystyle\frac{1}{2} \times \displaystyle\frac{2}{2 x-1}$
donc
$F(x)=2 x+\displaystyle\frac{1}{2} \ln |2 x+1|-\displaystyle\frac{1}{2} \ln |2 x-1|$
$\begin{array}{ll}\displaystyle\int_{0}^{\frac{1}{4}} f(x) dx&=\left[2 x+\displaystyle\frac{1}{2} \ln |2 x+1|-\displaystyle\frac{1}{2} \ln |2 x-1|\right]_{0}^{\frac{1}{4}}\\&=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2} \ln \displaystyle\frac{3}{2}-\displaystyle\frac{1}{2} \ln \displaystyle\frac{1}{2}-\left(\displaystyle\frac{1}{2} \ln 1-\displaystyle\frac{1}{2} \ln 1\right)\\&=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2} \ln 3 \end{array}$
Exercice 15 :
Soient $a$ et $b$ deux réels.
On considère les fonctions $f$ et $F$ définies sur $I\!R$ par $f(x)=(x-1) e ^{-x}$ et $F(x)=(a x+b) e ^{-x}$
1) Déterminer les réels $a$ et $b$ tels que $F$ soit une primitive de $f$
2) En déduire $\displaystyle\int_{0}^{\ln (3)}(x-1) e^{-x} dx$
Réponse :
$F(x)=(a x+b) e^{-x}$
$\begin{array}{ll} F^{\prime}(x)&=a \times e ^{-x}+(a x+b) \times\left(- e ^{-x}\right)\\&=(a-a x-b) e ^{-x}\\&=(a-b-a x) e ^{-x} \end{array}$
On identifie avec l'expression de $f(x)=(x-1) e ^{-x}$:
$\left\{\begin{array}{l}a-b=-1 \\ -a=1\end{array} \Leftrightarrow\left\{\begin{array}{l}a=-1 \\ b=0\end{array}\right.\right.$
Donc $F(x)=-x e ^{-x}$ et
$\begin{array}{ll} \displaystyle\int_{0}^{\ln 3} f(x) dx&=F(\ln 3)-F(0)\\&=-\ln 3 e ^{-\ln 3}\\&=-\ln 3 e ^{\ln \displaystyle\frac{1}{3}}\\&=-\displaystyle\frac{\ln 3}{3}\end{array}$
III. Intégration par parties:
Théorème :
Soit $u$ et $v$ deux fonctions dérivables sur un intervalle $I,$ dont les dérivées $u'$ et $v'$ sont continues sur $I$
Pour tous réels $a$ et $b$ de $I$, $\int_{a}^{b} u(x) v^{\prime}(x) dx=[u(x) v(x)]_{a}^{b}-\int_{a}^{b} u^{\prime}(x) v(x) dx$
Preuve :
$\bullet$ $u$ et $v$ sont dérivables sur $I$ donc $u v$ est dérivable sur $I$, et $(u v)^{\prime}=u^{\prime} v+u v^{\prime},$ donc
$u v^{\prime}=(u v)^{\prime}-u^{\prime} v$
$\bullet$ $u, v, u$ ' et $v$ ' sont continues sur $I$, donc $u v^{\prime}, u$ 'v et $(u v)$ ' le sont aussi alors
$\begin{array}{ll} \int_{a}^{b} u(x) v^{\prime}(x) dx &=\int_{a}^{b}[(u v)^{\prime}(x)-u^{\prime}(x) v(x)] dx \\ &=\int_{a}^{b}(u v)^{\prime}(x) dx-\int_{a}^{b} u^{\prime}(x) v(x) dx \\ &=[u v(x)]_{a}^{b}-\int_{a}^{b} u^{\prime}(x) v(x) dx \end{array}$
Exemples:
Calculer $J=\int_{0}^{\pi} x \sin x dx$
Soit $x$ un réel strictement positif. Calculer $\int_{1}^{x} \ln t dt$
Calculer $J=\int_{0}^{\pi} x e^{x} dx$
On note $I=\int_{0}^{\pi} e ^{x} \sin x dx$ et $J=\int_{0}^{\pi} e ^{x} \cos x dx$
a. Démontrer que $I=-J$ et que $I=J+1+ e ^{\pi}$
b. En déduire les valeurs exactes de $I$ et de $J$
Exercice 16 :
À l'aide d'une intégration par parties, calculer les intégrales suivantes:
a) $\int_{0}^{\displaystyle\frac{\pi}{2}} x \sin x dx$
b) $\int_{0}^{2}(2-x) e ^{x} dx$
c) $\int_{1}^{ e } \ln (x) dx$
Réponse :
a) $\int_{0}^{\frac{\pi}{2}} x \sin x dx$
Posons: $u(x)=x$ et $v^{\prime}(x)=\sin x$
On a : $u^{\prime}(x)=1$ et $v(x)=-\cos x$
Les fonctions $u$, $v$, $u^{\prime}$ et $v^{\prime}$ sont continues sur $[0 ; \displaystyle\frac{\pi}{2}]$
Appliquons la formule d'intégration par parties :
$\begin{array}{ll} \int_{0}^{\frac{\pi}{2}} x \sin x dx &=[-x \cos x]_{0}^{\frac{\pi}{2}}-\int_{0}^{\frac{\pi}{2}}(-\cos x) dx \\ &=\left(-\displaystyle\frac{\pi}{2} \cos \displaystyle\frac{\pi}{2}\right)-(-0 \cos 0)+[\sin x]_{0}^{\frac{\pi}{2}}\\&=\sin \displaystyle\frac{\pi}{2}-\sin 0=1 \end{array}$
b) $\int_{0}^{2}(2-x) e^{x} dx$
Posons : $u(x)=2-x$ et $v^{\prime}(x)=e^{x}$
On a : $u^{\prime}(x)=-1$ et $v(x)=e^{x}$
Les fonctions $u$, $v$, $u^{\prime}$ et $v^{\prime}$ sont continues sur $[0 ; 2]$
Appliquons la formule d'intégration par parties :
$\begin{array}{ll} \int_{0}^{2}(2-x) e^{x} dx&=[(2-x) e^{x}]_{0}^{2}-\int_{0}^{2}\left(-e^{x}\right) dx\\&=-2 e^{0}+[e^{x}]_{0}^{2}\\&=-2+e^{2}-e^{0}\\&=e^{2}-3\end{array}$
c) $\int_{1}^{e} \ln (x) dx$
Posons : $u(x) =\ln x$ et $v^{\prime}(x)=1$
On a : $u^{\prime}(x)=\displaystyle\frac{1}{x}$ et $v(x)=x$
Les fonctions $u$, $v$, $u^{\prime}$ et $v^{\prime}$ sont continues sur $[1 ; e]$
Appliquons la formule d'intégration par parties :
$\begin{array}{ll}\int_{1}^{e} \ln (x) dx &=[x \ln (x)]_{1}^{e}-\int_{1}^{e} \displaystyle\frac{1}{x} x dx\\&= e \ln (e)-1 \ln (1)-\int_{1}^{e} 1 dx\\&=e-[x]_{1}^{e}=e-(e-1)=1\end{array}$
Exercice 17 :
À l'aide d'une intégration par parties, donner une primitive sur $] 0 ;+\infty[$ de la fonction $f$ définie sur $]0 ;+\infty[$ par $f(x)=x^{2} \ln (x)$
Réponse :
$f(x)=x^{2} \ln (x)$ pour $x \in] 0 ;+\infty[$
Posons : $u(x)=\ln x$ et $v^{\prime}(x)=x^{2}$
on a : $u^{\prime}(x)=\displaystyle\frac{1}{x}$ et $v(x)=\displaystyle\frac{x^{3}}{3}$
les fonctions $u$, $v$, $u^{\prime}$ et $ v^{\prime}$ sont continues sur $] 0 ;+\infty[$
Appliquons la formule d'intégration par parties :
$\begin{array}{ll}\int x^{2} \ln (x) dx &=[\displaystyle\frac{x^{3}}{3} \ln (x)]-\int \frac{x^{2}}{3} dx \\&=\displaystyle\frac{x^{3}}{3} \ln (x)-[\displaystyle\frac{1}{3} \times \displaystyle\frac{x^{3}}{3}] \end{array}$
Une primitive sur $] 0 ;+\infty[$ de $f$ est la fonction $F$ définie sur $] 0 ;+\infty[$ par $F(x)=\displaystyle\frac{x^{3}}{3} \ln (x) \displaystyle\frac{x^{3}}{3}$
Exercice 18 :
Calculez l'intégrale $I$ en utilisant la formule d'intégration par parties:
1) $I=\int_{-1}^{0} x e^{x} d x$
2) $I=\int_{-1}^{0}(x+2) e^{x} d x$
3) $I=\int_{-1}^{0}(x+2) e^{x+1} d x$
Réponse :
$\begin{aligned}1)\ I&=\int_{-1}^{0} x e^{x} d x\\&=\int_{-1}^{0} u(x) v^{\prime}(x) d x\end{aligned}$
Posons : $u(x)=x$ et $v^{\prime}(x)=e^{x}$
on a : $u^{\prime}(x)=1$ et $v(x)=e^{x}$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues
D'après la formule d'intégration par parties,
$\begin{aligned}I&=[u(x) v(x)]_{-1}^{0}-\int_{-1}^{0} u^{\prime}(x) v(x) d x\\&=\left[x e^{x}\right]_{-1}^{0}-\int_{-1}^{0} 1 \times e^{x} d x\\&=0-(-1) e^{-1}-\left[e^{x}\right]_{-1}^{0}\\&=\frac{1}{e}-\left(1-\frac{1}{e}\right)\\&=\frac{2}{e}-1\end{aligned}$
$\begin{aligned}2)\ I&=\int_{-1}^{0}(x+2) e^{x} d x\\&=\int_{-1}^{0} u(x) v^{\prime}(x) d x\end{aligned}$
Posons : $u(x)=x+2$ et $v^{\prime}(x)=e^{x}$
on a : $u^{\prime}(x)=1$ et $v(x)=e^{x}$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues
D'après la formule d'intégration par parties,
$\begin{aligned}I&=[u(x) v(x)]_{-1}^{0}-\int_{-1}^{0} u^{\prime}(x) v(x) d x\\&=\left[(x+2) e^{x}\right]_{-1}^{0}-\int_{-1}^{0} 1 \times e^{x} d x\\&=2-(1) e^{-1}-\left[e^{x}\right]_{-1}^{0}\\&=2-\frac{1}{e}-\left(1-\frac{1}{e}\right)\\&=1\end{aligned}$
$\begin{aligned}3)\ I&=\int_{-1}^{0}(x+2) e^{x+1} d x\\&=\int_{-1}^{0} u(x) v^{\prime}(x) d x \end{aligned}$
Posons : $u(x)=x+2$ et $v^{\prime}(x)=e^{x+1}$
on a : $u^{\prime}(x)=1$ et $v(x)=e^{x+1}$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues
D'après la formule d'intégration par parties,
$\begin{aligned}I&=[u(x) v(x)]_{-1}^{0}-\int_{-1}^{0} u^{\prime}(x) v(x) d x\\&=\left[(x+2) e^{x+1}\right]_{-1}^{0}-\int_{-1}^{0} 1 \times e^{x+1} d x\\&=2 e-(1) e^{1}-\left[e^{x+1}\right]_{-1}^{0}\\&=e-(e-1)=1\end{aligned}$
Exercice 19 :
Calculez l'intégrale $I$ en utilisant deux fois le théorème de l'intégration par parties:
1) $I=\int_{0}^{\pi} e^{x} \sin x d x$
2) $I=\int_{0}^{\pi} e^{2 x} \cos x d x$
Réponse :
$\begin{aligned}1)\ I&=\int_{0}^{\pi} e^{x} \sin x d x\\&=\int_{0}^{\pi} u(x) v^{\prime}(x) d x\end{aligned}$
Posons : $u(x)=e^{x}$ et $v^{\prime}(x)=\sin x$
on a : $u^{\prime}(x)=e^{x}$ et $v(x)=-\cos x$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues
D'après la formule d'intégration par parties,
$\begin{aligned}I&=[u(x) v(x)]_{0}^{\pi}-\int_{0}^{\pi} u^{\prime}(x) v(x) d x\\&=\left[-e^{x} \cos x\right]_{0}^{\pi}-\int_{0}^{\pi} e^{x} \times(-\cos x) d x\\&=e^{\pi}+1+\int_{0}^{\pi} e^{x} \cos x d x\end{aligned}$
On calcule $J=\int_{0}^{\pi} e^{x} \cos x d x$ en effectuant une deuxième intégration par parties :
$\begin{aligned}J&=\int_{0}^{\pi} e^{x} \cos x d x\\&=\int_{0}^{\pi} u(x) v^{\prime}(x) d x\end{aligned}$
Posons : $u(x)=e^{x}$ et $v^{\prime}(x)=\cos x$
on a : $u^{\prime}(x)=e^{x}$ et $v(x)=\sin x$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues
D'après la formule d'intégration par parties,
$\begin{aligned}J&=[u(x) v(x)]_{0}^{\pi}-\int_{0}^{\pi} u^{\prime}(x) v(x) d x\\&=\left[e^{x} \sin x\right]_{0}^{\pi}-\int_{0}^{\pi} e^{x} \sin x d x\\&=0-0-I \end{aligned}$
On aboutit donc à l'équation
$I=e^{\pi}+1-I$
c'est-à-dire $2 I=e^{\pi}+1$ et on conclut ainsi que $I=\frac{e^{\pi}+1}{2}$
$\begin{aligned}2)\ I&=\int_{0}^{\pi} e^{2 x} \cos x d x\\&=\int_{0}^{\pi} u(x) v^{\prime}(x) d x\end{aligned}$
Posons : $u(x)=e^{2 x}$ et $v^{\prime}(x)=\cos x$
on a : $u^{\prime}(x)=2 e^{2 x}$ et $v(x)=\sin x$
les fonctions $u$, $v$ , $u^{\prime}$ et $v^{\prime}$ sont continues sur
D'après la formule d'intégration par parties,
$\begin{aligned}I&=[u(x) v(x)]_{0}^{\pi}-\int_{0}^{\pi} u^{\prime}(x) v(x) d x\\&=\left[e^{2 x} \sin x\right]_{0}^{\pi}-\int_{0}^{\pi} 2 e^{2 x} \sin x d x\\&=0-0-\int_{0}^{\pi} 2 e^{2 x} \sin x d x\end{aligned}$
On calcule $J=\int_{0}^{\pi} 2 e^{2 x} \sin x d x$ en effectuant une deuxième intégration par parties:
$J=\int_{0}^{\pi} 2 e^{2 x} \sin x d x=\int_{0}^{\pi} u(x) v^{\prime}(x) d x$ où $u(x)=2 e^{2 x} \Rightarrow u^{\prime}(x)=4 e^{2 x} \quad$ et $\quad v^{\prime}(x)=\sin x \Rightarrow v(x)=-\cos x$ sont continument dérivables.
D'après la formule d'intégration par parties,
$\begin{aligned}J&=[u(x) v(x)]_{0}^{\pi}-\int_{0}^{\pi} u^{\prime}(x) v(x) d x\\&=\left[-2 e^{2 x} \cos x\right]_{0}^{\pi}-\int_{0}^{\pi} 4 e^{2 x}(-\cos x) d x\\&=2 e^{2 \pi}+2+4 \int_{0}^{\pi} e^{2 x} \cos x d x\\&=2 e^{2 \pi}+2+4 I \end{aligned}$
On aboutit donc à l'équation
$I=-2 e^{2 \pi}-2-4 I$
c'est-à-dire $5 I=-2 e^{2 \pi}-2$ et on conclut ainsi que $I=-\frac{2}{5}\left(e^{2 \pi}+1\right)$
Exercice 20 :
On considère les intégrales $I=\int_{0}^{\pi} e ^{x} \sin (x) dx$ et $J=\int_{0}^{\pi} e ^{x} \cos (x) dx$
a) En intégrant $I$ puis $J$ par parties, démontrer que $I=-J$ puis que $I=J+e^{\pi}+1$
b) Déterminer $I$ et $J$ par résolution d'un système.
Réponse :
$I=\int_{0}^{\pi} e^{x} \sin (x) dx$ et $J=\int_{0}^{\pi} e^{x} \cos (x) dx$
a) En appliquant à $J$ la formule d'intégration par parties $\int u v^{\prime}=[u v]-\int u^{\prime} v$ avec
$u(x)=\cos x$ et $v^{\prime}(x)=e^{x}$, les fonctions $u$, $v$, $u$ 'et $v^{\prime}$ étant continues sur $[0 ; \pi]$, on obtient :
$\begin{aligned}J&=[(\cos x) e^{x}]_{0}^{\pi}-\int_{0}^{\pi}(-\sin x) e^{x} dx\\&=-e^{\pi}-1+I\end{aligned}$
donc $I=J+e^{\pi}+1$
b) Pour déterminer $I$ et $J$, on résout le système
$(S):\left\{\begin{array}{l}I=-J \\ I=J+e^{\pi}+1\end{array}\right.$
$(S) \Leftrightarrow\left\{\begin{array}{l}J=-I \\ I=-I+e^{\pi}+1\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}J=-I \\ 2 I=e^{\pi}+1\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}I=\displaystyle\frac{e^{\pi}+1}{2} \\ J=-\displaystyle\frac{e^{\pi}+1}{2}\end{array}\right.$
Exercice 21 :
Soit $n$ un entier naturel et $I_{n}=\int_{0}^{1} x^{n} e ^{1-x} dx$
a) Calculer $I_{1}$
b) Établir une relation entre $I_{n+1}$ et $I_{n}$
c) En déduire $I_{3}$
Réponse :
$I_{n}=\int_{0}^{1} x^{n} e^{1-x} dx$ pour $n$ entier naturel
$\begin{array}{ll} a)\ I_{1}&=\int_{0}^{1} x e^{1-x} dx\\&=[-x e^{1-x}]_{0}^{1}-\int_{0}^{1}\left(-e^{1-x}\right) dx\\&=-1+[-e^{1-x}]_{0}^{1}\\&=-1-1+e=e-2 \end{array}$
$\begin{array}{ll}b)\ I_{n+1}&=\int_{0}^{1} x^{n+1} e^{1-x} dx\\&=[-x^{n+1} e^{1-x}]_{0}^{1}-\int_{0}^{1}(n+1) x^{n}\left(-e^{1-x}\right) dx\\&=-1+(n+1) \int_{0}^{1} x^{n} e^{1-x} dx \end{array} $
donc $I_{n+1}=(n+1) I_{n}-1$
c) On calcule d'abord $I_{2}$:
$I_{2}=3 I_{1}-1=3 e-7$;
on en déduit $I_{3}$:
$I_{3}=4 I_{2}-1=12 e-29$
Exercice 22 :
À l'aide d'une double intégration par parties, calculer
a) $I=\int_{0}^{3} x^{2} e ^{-2 x} dx$
b) $I=\int_{0}^{\pi} x^{2} \cos (x) dx$
Réponse :
a) $I=\int_{0}^{3} x^{2} e^{-2 x} dx$
En appliquant la formule d'intégration par parties $\int u v^{\prime}=[u v]-\int u^{\prime} v$
avec $u(x)=x^{2}$ et $v^{\prime}(x)=e^{-2 x},$ les fonctions $u$, $v$, $u^{\prime}$ et $v^{\prime}$ étant continues sur $[0 ; 3],$ on obtient :
$\begin{array}{ll} I&=[x^{2}\left(-\displaystyle\frac{1}{2} e^{-2 x}\right)]_{0}^{3}-\int_{0}^{3} 2 x\left(-\displaystyle\frac{1}{2} e^{-2 x}\right) dx\\&=-\displaystyle\frac{9}{2} e^{-6}+\int_{0}^{3} x e^{-2 x} dx \end{array}$
Intégrons de nouveau par parties $\int_{0}^{3} x e^{-2 x} dx$ avec $u(x)=x$ et $v^{\prime}(x)=e^{-2 x}$
$\begin{array}{ll} \int_{0}^{3} x e^{-2 x} dx&=[-\displaystyle\frac{1}{2} x e^{-2 x}]_{0}^{3}-\int_{0}^{3}\left(-\displaystyle\frac{1}{2} e^{-2 x}\right) dx\\&=-\displaystyle\frac{3}{2} e^{-6}+[-\displaystyle\frac{1}{4} e^{-2 x}]_{0}^{3}\\&=-\displaystyle\frac{7}{4} e^{-6}+\displaystyle\frac{1}{4} \end{array}$
On en déduit :
$\begin{aligned}I&=-\displaystyle\frac{9}{2} e^{-6}-\displaystyle\frac{7}{4} e^{-6}+\displaystyle\frac{1}{4}\\&=-\displaystyle\frac{25}{4} e^{-6}+\displaystyle\frac{1}{4}\end{aligned}$
b) $I=\int_{0}^{\pi} x^{2} \cos (x) dx$
En appliquant la formule d'intégration par parties $\int u v^{\prime}=[u v]-\int u^{\prime} v$ avec
$u(x)=x^{2}$ et $v^{\prime}(x)=\cos x$, les fonctions $u$, $v$, $u^{\prime}$ et $v^{\prime}$ étant continues sur $[0 ; \pi],$ on obtient :
$\begin{array}{ll} I&=[x^{2} \sin x]_{0}^{\pi}-\int_{0}^{\pi} 2 x \sin x dx\\&=-2 \int_{0}^{\pi} x \sin x dx \end{array}$
Intégrons de nouveau par parties $\int_{0}^{\pi} x \sin x dx$ avec $u(x)=x$ et $v^{\prime}(x)=\sin x$
$\begin{aligned}\int_{0}^{\pi} x \sin x dx&=[x \cos x]_{0}^{\pi}-\int_{0}^{\pi}(-\cos x) dx\\&=1+[\sin x]_{0}^{\pi}\\&=1\end{aligned}$
On en déduit : $I=-2 \times 1=-2$
III. Calcul d’aires:
Exercice 23 :
Associer chaque intégrale au schéma qui lui correspond (pour cet exercice, les aires des parties du plan situées sous l’axe des abscisses sont comptées négativement).
a)
b)
c)
d)
1) $\int_{-1}^{2} f(x) dx$
2) $\int_{0}^{2} f(x) dx$
3) $\int_{-1}^{2}|f(x)| dx$
4) $\int_{1}^{2} f(x) dx$
Réponse :
Le schéma a) correspond à l'intégrale 1.
Le schéma b) correspond à l'intégrale 3.
Le schéma c) correspond à l'intégrale 4.
Le schéma d) correspond à l'intégrale 2.
Exercice 24 :
On a tracé dans le repère ci-dessous la courbe représentative de la fonction $f$.
On suppose connues les aires $A_{1}$, $A_{2}$, $A_{3}$, $A_{4}$ et $A_{5}$.
a) Avec ces valeurs, exprimer les intégrales suivantes:
$I_{1}=\int_{-6}^{-1,5} f(x) dx$ ,
$I_{2}=\int_{-1,5}^{2} f(x) dx$ et
$I_{3}=\int_{0}^{3} f(x) dx$
b) À l'aide d'intégrales, exprimer la somme $A_{1}+A_{2}+A_{3}$
Réponse :
a) $I_{1}=-A_{1}+A_{2}$,
$I_{2}=-A_{3}-A_{4}$ et
$I_{3}=A_{5}-A_{4}$
b)
$\begin{array}{ll}A_{1}+A_{2}+A_{3}&=\int_{-6}^{0}|f(x)| dx\\&=\int_{-5}^{-1,5} f(x) dx-\int_{-6}^{-5} f(x) dx-\int_{-1,5}^{0} f(x) dx\end{array}$
Exercice 25 :
Les aires $A_{1}, A_{2}, A_{3}, A_{4}, A_{5}$ et $A_{6}$ sont connues.
a) Exprimer les intégrales suivantes à l'aide de ces valeurs.
$I_{1}=\int_{-1}^{1} f(x) dx$
$I_{2}=\int_{-1}^{3} g(x) dx$
$I_{3}=\int_{-1}^{3}[f(x)-g(x)] dx$
$I_{4}=\int_{-1}^{2}|f(x)-g(x)| dx$
b) Exprimer à l'aide d'intégrales la somme $A_{4}+A_{5}$
Réponse :
a) $I_{1}=A_{1}+A_{3}$
$I_{2}=A_{3}+A_{4}+A_{5}$
$I_{3}=A_{1}+A_{2}-A_{6}$
$I_{4}=A_{1}+A_{2}+A_{6}$
b) $A_{4}+A_{5}=\int_{1}^{2} g(x) dx+\int_{2}^{3} f(x) dx$
Exercice 26 :
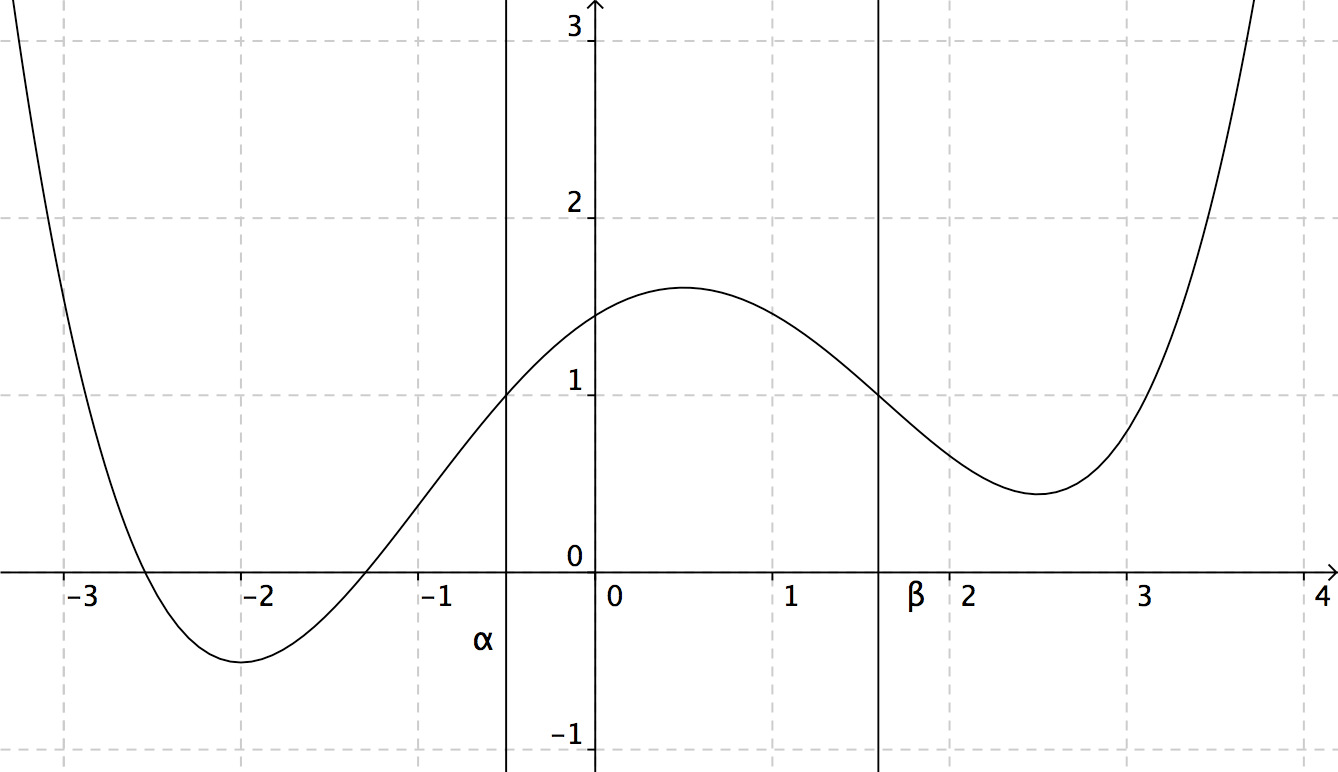
On a tracé ci-dessous la courbe représentative d'une fonction $f$ et deux droites d'équations respectives $x=\alpha$ et $x=\beta$
a) Colorier en rouge la partie du plan dont l'aire est donnée par $\int_{2}^{3} f(x) dx$
b) Colorier en bleu la partie du plan dont l'aire est donnée par $\int_{-2}^{1}|f(x)| dx$
c) Colorier en vert la partie du plan dont l'aire est donnée par $\int_{\alpha}^{\beta}|f(x)-1| dx$
Réponse :
a) $\int_{2}^{3} f(x) dx$ est l'aire de la partie du plan coloriée en rouge.
b) $\int_{-2}^{1}|f(x)|$ d $x$ est l'aire de la partie du plan coloriée en bleu.
c) $\int_{\alpha}^{\beta}|f(x)-1| dx$ est l'aire de la partie du plan coloriée en vert.
Exercice 27:
On a tracé dans le repère ci-dessous les courbes représentatives des fonctions $f$, $g$ et $h$ définies par:
$f(x)=\displaystyle\frac{1}{x}$, $g(x)=\sqrt{x}$ et $h(x)=\displaystyle\frac{3}{4} x-1$
a) Exprimer avec l'aide des intégrales l'aire rouge $A_{r o u g e}$ et la calculer.
b) Calculer $A_{\text {bleue}}=\int_{2}^{4}\left(\sqrt{x}-\displaystyle\frac{3}{4} x+1\right) dx$
c) En déduire l'aire coloriée sur la figure en unités d'aire.
Réponse :
a)
$\begin{array}{ll}A_{\text {rouge}}&=\int_{1}^{2}[g(x)-f(x)] dx\\&=\int_{1}^{2}\left[\sqrt{x}-\displaystyle\frac{1}{x}\right] dx\\&=\int_{1}^{2} \sqrt{x} dx-\int_{1}^{2} \displaystyle\frac{1}{x} dx\end{array}$
Sur l'intervalle $[1 ; 2]$, une primitive de la fonction $g$ est $G(x)=\displaystyle\frac{2}{3} x^{\frac{3}{2}}$
Et une primitive de la fonction $f$ est $F(x)=\ln x$
Donc l'aire est égale à
$\begin{array}{ll}A_{\text {rouge}}&=\left[\displaystyle\frac{2}{3} x^{\frac{3}{2}}\right]_{1}^{2}-[\ln x]_{1}^{2}\\&=\displaystyle\frac{2}{3} 2^{\frac{3}{2}}-\displaystyle\frac{2}{3}-(\ln 2-\ln 1)\\&=\displaystyle\frac{4 \sqrt{2}-2}{3}-\ln 2\end{array}$
b)
$\begin{array}{ll}A_{\text {bleue }}&=\int_{2}^{4}\left(\sqrt{x}-\displaystyle\frac{3}{4} x+1\right) dx\\&=\int_{2}^{4} \sqrt{x} dx-\int_{2}^{4}\left(\displaystyle\frac{3}{4} x-1\right) dx\end{array}$
Sur l'intervalle $[1 ; 2],$ une primitive de la fonction $h$ est $H(x)=\displaystyle\frac{3}{8} x^{2}-x$
Donc
$\begin{array}{ll}A_{\text {bleue}}&=\left[\displaystyle\frac{2}{3} x^{\frac{3}{2}}\right]_{2}^{4}-\left[\displaystyle\frac{3}{8} x^{2}-x\right]_{2}^{4}\\&=\displaystyle\frac{2}{3} \times 8-\displaystyle\frac{2}{3} \sqrt{8}-\left(\displaystyle\frac{3}{8} \times 16-4-\displaystyle\frac{3}{8} \times 4+2\right)\\&=\displaystyle\frac{17-8 \sqrt{2}}{6}\end{array}$
c) L'aire de la partie coloriée est $A_{\text {rouge}}+A_{\text {bleue}}=\displaystyle\frac{13}{6}-\ln 2$ unités d'aire.
Exercice 28:
1. On a tracé dans le repère ci-dessous la courbe représentative de la fonction
$f(x)= \displaystyle \frac{1}{3} x^{2}-x$
a) Exprimer avec une intégrale l'aire verte $V$.
Calculer $V$.
b) Exprimer avec une intégrale l'aire bleue $B$.
Calculer $B$.
2. On a tracé dans le repère ci-dessous la courbe représentative de la fonction $g(x)= \displaystyle \frac{3 x^{2}}{\left(x^{3}+1\right)^{2}}$ .
$m$ désigne un réel strictement positif et $A(m)$ est l'aire de la partie du plan situé entre les droites d'équation $x=-\displaystyle \frac{1}{2}$, $x=m,$ l'axe des abscisses et la courbe représentative de la fonction $g$.
Cette aire est fonction de $m$
Calculer l'aire $A(m)$ et déterminer la limite de $A(m)$ lorsque $m$ tend vers l'infini.
Réponse :
1. a) $V=\int_{-2}^{0} f(x) dx$
Une primitive de la fonction $f$ est $F(x)=\displaystyle\frac{1}{9} x^{3}-\displaystyle\frac{1}{2} x^{2}$
Donc
$\begin{array}{ll}\int_{-2}^{0} f(x) dx&=[F(x)]_{-2}^{0}\\&=F(0)-F(2)\\&= \displaystyle \frac{8}{9}+\displaystyle\frac{4}{2}\\&=\displaystyle\frac{8}{9}+2\\&=\displaystyle\frac{26}{9}\end{array}$
L'aire verte $V$ est égale à $V=\displaystyle\frac{26}{9} \ u.a$.
b) $B=\int_{0}^{5}|f(x)| dx=\int_{0}^{3}-f(x) dx+\int_{3}^{5} f(x) dx$
Une primitive de la fonction $f$ est $F(x)= \displaystyle \frac{1}{9} x^{3}-\displaystyle\frac{1}{2} x^{2}$
Donc
$\begin{array}{ll} \int_{0}^{3}-f(x) dx=[-F(x)]_{0}^{3}=-F(3)+F(0)=-\displaystyle \frac{27}{9}+\frac{9}{2}= \frac{3}{2}\end{array}$
Et
$\begin{array}{ll} \int_{3}^{5} f(x) dx&=[F(x)]_{3}^{5}\\&=F(5)-F(3)\\&=\displaystyle\frac{125}{9}-\displaystyle\frac{25}{2}-\displaystyle\frac{27}{9}+\displaystyle\frac{9}{2}\\&=\displaystyle\frac{26}{9}\end{array}$
Donc l'aire bleue est égale à
$B=\displaystyle \frac{3}{2}+\displaystyle\frac{26}{9}=\displaystyle\frac{79}{18}$ u.a
2. $A(m)=\int_{-0,5}^{m} g(x) dx .$
La fonction $g$ est de la forme $g(x)=\displaystyle\frac{u^{\prime}(x)}{u^{2}(x)}$ où $u(x)=x^{2}+1$
La fonction $G(x)=\displaystyle\frac{-1}{x^{3}+1}$ est une primitive de la fonction $g$
$\begin{array}{ll}A(m)&=\int_{-0,5}^{m} g(x) dx\\&=[G(x)]_{-0,5}^{m}\\&=G(m)-G(-0,5)\\&= \displaystyle \frac{-1}{m^{3}+1}+\displaystyle \displaystyle\frac{1}{0,125+1}\\&=\displaystyle \frac{8}{9}-\displaystyle \frac{1}{m^{3}+1}\end{array}$
$A(m)= \displaystyle \frac{8}{9}-\displaystyle \frac{1}{m^{3}+1}$ unités d'aire
$\displaystyle \lim _{m \rightarrow+\infty}\left(m^{3}+1\right)=+\infty$
Donc $\displaystyle \lim _{m \rightarrow+\infty} A(m)= \displaystyle \frac{8}{9} \text { u.a. }$
Exercice 29 :
Soit la fonction $f(x)=x^{4}-3 x^{2}+2$ définie sur $[-2 ; 2]$, représentée ci-dessous dans un repère orthogonal.
Les unités graphiques sont $2 \mathrm{cm}$ sur l'axe $(O x)$ et $1 \mathrm{cm}$ sur l'axe $(O y)$
Calculer l'aire, en $\mathrm{cm}^{2},$ du domaine $D$ coloré.
Réponse :
Il faut déterminer les bornes.
On résout $f(x)=0$ .
Les solutions sont ${-\sqrt{2} ;-1 ; 1 ; \sqrt{2}}$
L'aire du domaine $D$ est
$\begin{array}{ll}A&=\displaystyle \int_{-\sqrt{2}}^{\sqrt{2}}|f(x)| dx\\&=-\int_{-\sqrt{2}}^{-1} f(x) dx+\int_{-1}^{1} f(x) dx-\int_{1}^{\sqrt{2}} f(x) dx \ unités d'aire\end{array}$
Une primitive de la fonction $f$ est $F(x)= \displaystyle \frac{1}{5} x^{5}-x^{3}+2 x$ .
$F$ est une fonction impaire.
$\begin{array}{l} A&=-[F(x)]_{-\sqrt{2}}^{-1}+[F(x)]_{-1}^{1}-[F(x)]_{1}^{\sqrt{2}} \\ &=-F(-1)+F(-\sqrt{2})+F(1)-F(-1)-F(\sqrt{2})+F(1)\\&=4 F(1)-2 F(\sqrt{2}) \\ &=4\left(\displaystyle \frac{1}{5}-1+2\right)-2\left(\displaystyle \frac{\sqrt{2}^{5}}{5}-\sqrt{2}^{3}+2 \sqrt{2}\right)\\&= \displaystyle\frac{24-8 \sqrt{2}}{5} \end{array}$
l'unité d'aire est de $2 \mathrm{cm}^{2}$ donc l'aire du domaine $D$ est $\displaystyle \frac{48-16 \sqrt{2}}{5} \approx 5,07 \mathrm{cm}^{2}$










Commentaires
Enregistrer un commentaire