Exercices corrigés nombres complexes

بسم الله الرحمن الرحيم 

•    Correction Exercice  لمشاهدة الحل انقر  على 
•  Correction Exercice  لإخفاء الحل انقر مرة ثانية على
• للانتقال لموضوع آخر ابحث في القائمة أعلاه
• لمشاهدة الأسطر الطويلة قم بتدوير الهاتف عرضيا 

Exercice 1
Déterminer le conjugué de chaque nombre complexe et donner sa forme algébrique.
1) $ z = (3+i)(-13 – 2i) $
2) $z=i(1-i)^3$
3) $z = \dfrac{2 – 3i}{8 + 5i}$
4) $z=\dfrac{2}{i + 1}-\dfrac{3}{1-i}$

🔻Correction Exercice 1

1)
$\begin{array}{ll} \overline{z} &= \overline{(3+i)(-13 – 2i)} \\\\&= (3 – i)(-13 + 2i) \\\\&=-39 +6i + 13i + 2 \\\\&=-37 + 19i\end{array}$
2)
$\begin{array}{ll} \overline{z}& = \overline{i(1-i)^3}\\\\ &= -i(1 + i)^3 \\\\ &=-i(1+ i)(1 + i)^2 \\\\ &= -i(1 + i)(1 + 2i – 1) \\\\ &= (-i + 1)(2i) \\\\ &=2 + 2i \end{array}$
3)
$\begin{array}{ll} \overline{z} &= \overline{\left(\dfrac{2 – 3i}{8 + 5i}\right)} \\\\ & = \dfrac{2 + 3i}{8 – 5i} \\\\ & = \dfrac{2 + 3i}{8 – 5i} \times \dfrac{8 + 5i}{8 + 5i}\\\\ & = \dfrac{16 + 10i + 24i – 15}{8^2 + 5^2} \\\\ & =\dfrac{1 + 34i}{89} \end{array}$
4)
$\begin{array} {ll} \overline{z} &= \overline{\dfrac{2}{i + 1}-\dfrac{3}{1-i}} \\\\ &=\overline{\left(\dfrac{2(1 – i) – 3(i + 1)}{(i + 1)(1 – i)}\right)} \\\\ &=\overline{\left(\dfrac{2 – 2i – 3i – 3}{1^2 + 1^2}\right)} \\\\ &=\overline{\dfrac{-1 – 5i}{2}}\\\\ &=\dfrac{-1 + 5i}{2} \end{array}$

Exercice 2
Mettre chaque nombre complexe sous sa forme algébrique.
1) $z = \dfrac{2 + i}{3 + i}$
2) $z = \dfrac{(2+i)(1 – 4i)}{i + 1}$

🔻Correction Exercice 2

1)
$\begin{array}{ll} z &= \dfrac{2 + i}{3 + i} \\\\ &= \dfrac{2 + i}{3 + i} \times \dfrac{3 – i}{3 – i} \\\\ &= \dfrac{6 -2i + 3i + 1}{3^2 + 1^2} \\\\ &= \dfrac{7 + i}{10} \end{array}$
2)
$\begin{array}{ll} z &=\dfrac{(2+i)(1 – 4i)}{i + 1} \\\\ &= \dfrac{2 – 8i + i + 4}{i + 1} \\\\ &= \dfrac{6 – 7i}{i + 1} \times \dfrac{-i + 1}{-i + 1} \\\\ &=\dfrac{-6i + 6 – 7 – 7i}{1^2 + 1^2}\\\\ &=\dfrac{-1 -13i}{2} \end{array}$

Exercice 3
Résoudre dans $\mathbb{C}$ chacune des équations suivantes :
1) $2z^2 – 6z + 5=0$
2) $z^2+z+1=0$
3) $ z^2 + 2\overline{z} + 1 = 0 $

🔻Correction Exercice 3

1) $2z^2 – 6z + 5=0$
On calcule le discriminant : $\Delta = (-6)^2 – 4 \times 2 \times 5 = -4 < 0$
L’équation possède donc deux racines complexes :
$ z_1 = \dfrac{6 – i\sqrt{4}}{4} = \dfrac{3 – i}{2}$ et $z_2 = \overline{z_1} = \dfrac{3 + i}{2}$
2) $ z^2+z+1=0$
On calcule le discriminant : $\Delta = 1^2 – 4 = -3 < 0$
L’équation possède donc deux racines complexes :
$z_1 = \dfrac{-1 – i\sqrt{3}}{2}$ et $z_2 = \overline{z_1} = \dfrac{-1 + i\sqrt{3}}{2}$
3) $z^2 + 2\overline{z} + 1 = 0$
Attention, il ne s’agit pas d’une équation du second degré “classique”.
On doit donc passer par la forme algébrique de $z = x + i y$.
On obtient ainsi :
$\begin{array}{ll} z^2 + 2\overline{z} + 1 = 0 & \Leftrightarrow (x + i y)^2 + 2(x – i y) + 1 = 0\\\\ & \Leftrightarrow x^2 – y^2 + 2i xy + 2x – 2i y + 1 = 0\\\\ & \Leftrightarrow x^2 – y^2 + 2x + 1 + i(2xy – 2y) = 0 \end{array}$
On doit donc résoudre le système :
$\begin{array}{ll} \begin{cases} x^2 – y^2 + 2x + 1 = 0 \\2xy – 2y = 0 \end{cases} & \Leftrightarrow \begin{cases} (x + 1)^2 – y^2 = 0\\\\2y(x – 1) = 0 \end{cases}\\\\ & \Leftrightarrow \begin{cases} (x + 1)^2 – y^2 = 0 \\\\y = 0 \text( ou ) x = 1 \end{cases} \end{array}$
Si $y = 0 $alors en remplaçant dans la première équation, on trouve $ (x + 1)^2 =0$ soit $x = -1$.
Si $x = 1 $alors en remplaçant dans la première équation, on trouve $4 -y ^2 = 0 $soit $y = 2 $ou $y= -2$.
Les solutions de l’équation sont donc : $-1, 1 + 2i \ et\ 1 – 2i$.

Exercice 4
Soit $z = x + i y$, $x $et $y$ étant deux réels
tels que $ (x;y) \ne (1;0) $.
On pose $Z = \dfrac{z + 2i}{z – 1}$.
Déterminer l’ensemble des points d’affixe $z$ tel que :
1) $Z $soit un nombre réel.
2) $Z$ soit un imaginaire pur.

🔻Correction Exercice 4

1)
$\begin{array}{ll} Z &= \dfrac{z + 2i}{z – 1} \\\\ &= \dfrac{x + i y+ 2i}{x + i y – 1} \\\\ &= \dfrac{x + i(y + 2)}{x – 1 + i y} \\\\ &= \dfrac{x + i(y + 2)}{x – 1 + i y} \times \dfrac{x – 1 – i y}{x – 1 – i y} \\\\ &= \dfrac{x(x – 1) -i xy + i (y + 2)(x – 1) + y(y + 2)}{(x – 1)^2 + y^2}\\\\ &=\dfrac{x(x – 1) + y(y + 2) + i\left((y + 2)(x – 1) – xy\right)}{(x – 1)^2 + y^2} \end{array} $
2) On veut que $Z $soit un nombre réel.
Il faut donc que sa partie imaginaire soit nulle.
Cela signifie donc que :
$\dfrac{(y + 2)(x – 1) – xy}{(x – 1)^2 + y^2} = 0 $
$ \Leftrightarrow xy – y + 2x – 2 – xy = 0 $et $ (x;y) \ne (1;0) $
$\Leftrightarrow 2x – y – 2 = 0 $et $ (x;y) \ne (1;0) $
L’ensemble des points tel que $Z$ soit un nombre réel est donc la droite d’équation $2x – y – 2 = 0 $privée du point de coordonnées $ (1;0) $.
3) On veut que $Z$ soit un imaginaire pur.
Il faut donc que sa partie réelle soit nulle.
Cela signifie donc que :
$\dfrac{x(x – 1) + y(y + 2)}{(x – 1)^2 + y^2} = 0$
$\Leftrightarrow x^2 – x + y^2 + 2y = 0 \ et\ (x;y) \ne (1;0) $
$\Leftrightarrow \left(x – \dfrac{1}{2}\right)^2 – \dfrac{1}{4} + (y + 1)^2 – 1 = 0 \ et\ (x;y) \ne (1;0) $
$\Leftrightarrow \left(x – \dfrac{1}{2}\right)^2 + (y + 1)^2 = \dfrac{5}{4} et (x;y) \ne (1;0) $
L’ensemble des points tel que $Z$ soit un imaginaire pur est donc le cercle de centre $\left(\dfrac{1}{2};-1\right) $ et de rayon $\dfrac{\sqrt{5}}{2}$ privé du point de coordonnées $ (1;0) $.

Exercice 5
1) On considère un réel $b$.
Développer $\left(z^2+bz+4\right)\left(z^2-bz+4\right) $.
2) En déduire les solutions complexes de l’équation $z^4+16=0$.

🔻Correction Exercice 5

1)
$\begin{array}{ll} \left(z^2+bz+4\right)\left(z^2-bz+4\right)&=z^4-bz^3+4z^2+bz^3-b^2z^2+4bz+4z^2-4bz+16 \\&=z^4+\left(8-b^2\right)z^2+16 \end{array}$
2) Posons $b=2\sqrt{2}$ alors $b^2=8$.
Ainsi, d’après la question précédente, $\left(z^2+2\sqrt{2}z+4\right)\left(z^2-2\sqrt{2}z+4\right)=z^4+16$.
Un produit de facteurs est nul si, et seulementsi, un des facteurs au moins est nul.
Donc $z^4+16=0 \Leftrightarrow z^2+2\sqrt{2}z+4=0 $ou $z^2-2\sqrt{2}z+4=0$.
$\color{red}{\bullet\quad Pour\ z^2+2\sqrt{2}z+4=0}$
$\Delta=-8<0 br=""> Il y a donc deux solutions complexes :
$z_1=\dfrac{-2\sqrt{2}-i\sqrt{8}}{2}=-\sqrt{2}-i\sqrt{2}$ et $z_2=\overline{z_1}=-\sqrt{2}+i\sqrt{2}$
$\color{red}{\bullet\quad Pour\ z^2-2\sqrt{2}z+4=0}$
$ \Delta=-8 < 0 $
Il y a donc deux solutions complexes :
$z_3=\dfrac{2\sqrt{2}-i\sqrt{8}}{2}=\sqrt{2}-i\sqrt{2}$ et $z_4=\overline{z_3}=\sqrt{2}+i\sqrt{2}$
Les solutions de l’équation $z^4+16=0$ sont donc$-\sqrt{2}-i\sqrt{2}$, $-\sqrt{2}+i\sqrt{2}$, $\sqrt{2}-i\sqrt{2}$ et $\sqrt{2}+i\sqrt{2}$

Exercice 6
Pour tout nombre complexe $z$ on pose $P(z)=z^4-1$.
1) Factoriser $P(z) $.
2) En déduire les solutions dans $\mathbb{C}$de l’équation $P(z)=0$.
3) En déduire les solutions dans $\mathbb{C}$ de l’équation $\left(\dfrac{2z+1}{z-1}\right)^4=1$

🔻Correction Exercice 6

1)
$\begin{array}{ll}z^4-1&=\left(z^2\right)^2-1^2 \\&=(z^2-1)(z^2+1) \\&=(z-1)(z+1)\left(z^2+1\right). \end{array}$
2) Un produit de facteurs est nul si, et seulement si, l’un de ses facteurs au moins est nul.
Donc
$\begin{array}{ll}P(z)=0 &\Leftrightarrow z-1=0 \ ou \ z+1=0 \ ou \ z^2+1=0 \\&\Leftrightarrow z=1 \ ou\ z=-1 \ ou\ z^2=-1\end{array}$
Les solutions de l’équation $P(z)=0$ sont donc $-1;1;i et -i$.
3) Si on pose $Z=\dfrac{2z+1}{z-1}$ L’équation $\left(\dfrac{2z+1}{z-1}\right)^4=1 $ est équivalente à $P(Z)=0$ $P(Z)=0\Leftrightarrow Z=1 \ ou\ Z=-1 \ ou\ Z=i \ ou\ Z=-i$.
Soit $a\in \mathbb{C}$
$\begin{array}{ll} Z=a &\Leftrightarrow \dfrac{2z+1}{z-1}=a \\&\Leftrightarrow 2z+1=a(z-1) \ et\ z\neq 1 \\&\Leftrightarrow 2z+1=az-a \ et\ z\neq 1 \\&\Leftrightarrow (2-a)z=-1-a \ et\ z\neq 1 \\&\Leftrightarrow z=\dfrac{-1-a}{2-a}\ et\ z\neq 1 \end{array}$
Par conséquent
$Z=1 \Leftrightarrow z=-2$
$Z=-1\Leftrightarrow z=0$
$Z=i \Leftrightarrow z=\dfrac{-1-i}{2-i}\Leftrightarrow z=\dfrac{-1-3i}{5}$
$Z=-i \Leftrightarrow z=\dfrac{-1+i}{+-i}\Leftrightarrow z=\dfrac{-1+3i}{5}$
Les solutions de l’équation initiale sont donc$-2;0;\dfrac{-1-3i}{5} $ et $ \dfrac{-1+3i}{5}$

Exercice 7
On considère dans $\mathbb{C}$ l’équation $(E):z^3-(1-i)z^2+(1-i)z+i=0$.
1) Montrer que $ (E) $ possède une unique solution imaginaire pure.
2) Résoudre dans $\mathbb{C}$ l’équation $(E) $.

🔻Correction Exercice 7

1) Soit $y\in \mathbb{R}$ alors $i y $ est un imaginaire pur.
Supposons que $i y$ soit une solution de $ (E) $.
Par conséquent :
$\begin{array}{ll} iy \ solution\ de\ (E)&\Leftrightarrow (i y)^3-(1-i)(iy)^2+(1-i)iy+i =0 \\&\Leftrightarrow-i y^3-(1-i)\times \left(-y^2\right)+iy+y+i =0 \\&\Leftrightarrow -iy^3+y^2-i y^2+i y+y+i =0 \\&\Leftrightarrow y^2+y+i\left(1+y-y^2-y^3\right)=0 \\&\Leftrightarrow\begin{cases}y(y+1)=0 \\1+y-y^2-y^3=0 \end{cases} \\&\Leftrightarrow\begin{cases}y=0 \ ou\ y=-1 \\1+y-y^2-y^3=0 \end{cases} \end{array}$
0 n’est pas solution de l’équation $1+y-y^2-y^3=0$
-1 est solution de l’équation $1+y-y^2-y^3=0$.
Par conséquent la seule solution imaginaire pure possible est $-i$
Vérifions que $-i $ est bien solution de $ (E) $
$ (-i)^3-(1-i)(-i)^2+(1-i)(-i)+i=i+1-i-i-1+i=0$
Donc $-i $ est l’unique solution imaginaire pure de l’équation $ (E) $.
2) Puisque $-i $ est solution de $ (E) $ on peut factoriser le polynôme par $ (z+i) $.
On cherche donc les nombres complexes $ a $ et $ b $ tels que :
$ (z+i)\left(z^2+az+b\right)=z^3-(1-i)z+(1-i)z+i $
$ \begin{array}{ll} (z+i)\left(z^2+az+b\right)&=z^3+az^2+bz+i z^2+ai z+bi \\&=z^3+(a+i)z^2+(b+ai)z+bi \end{array} $
Par identification on a donc $ a=-1 $ et $ b=1 $
Ainsi $ (E) \Leftrightarrow (z+i)\left(z^2-z+1\right)=0 $
On considère l’équation $ z^2-z+1=0 $
$\Delta = -3 < 0$
Il y a donc deux solutions complexes :
$z_1=\dfrac{1+i\sqrt{3}}{2}$ et $z_2=\dfrac{1-i\sqrt{3}}{2}$.
Les solutions de $(E)$ sont donc $-i, \dfrac{1+i\sqrt{3}}{2}$ et $\dfrac{1-i\sqrt{3}}{2}$.

Exercice 8
Résoudre dans $ \mathbb{C} $ l’équation $ 25+10z+z^2=16i $.

🔻Correction Exercice 8

On pose $ z=x+i y $
$ (E): 25+10z+z^2=16i $
$\begin{array}{ll} (E)&\Leftrightarrow 25+10(x+iy)+x^2-y^2+2i\ xy=16i\ \\ &\Leftrightarrow 25+10x+x^2-y^2+I \left(10y+2xy \right)=16i\\ &\Leftrightarrow (5+x)^2-y^2+i\ y(10+2x)=16i\\ &\Leftrightarrow \begin{cases}\ (5+x)^2-y^2=0\ \\y(10+2x)=16\end{cases}\\ &\Leftrightarrow\ \begin{cases}\ (5+x)^2=y^2\\y(10+2x)=16\end{cases}\\ &\Leftrightarrow\begin{cases}\ y=5+x\ ou\ y=-5-x\\y(10+2x)=16\end{cases}\ \\ &\Leftrightarrow\ \begin{cases}y=5+x\$5+x)(10+2x)=16\end{cases}\ ou\ \ \begin{cases}\ y=-5-x\$-5-x)(10+2x)=16\end{cases}\ \\ &\Leftrightarrow\ \begin{cases}\ y=5+x\\2x^2+20x+34=0\end{cases}\ ou\ \begin{cases}\ y=-5-x\\-2x^2-20x-66=0\end{cases}\ \\ &\Leftrightarrow\ \begin{cases}\ y=5+x\\x=-5+2\sqrt{2}\ \ ou\ x=-5-2\sqrt{2}\end{cases}\ \\ &\ \ il\ n’y\ a\ pas\ de\ solution\ réelles\ à\ -2x^2-20x-66=0\\ &\Leftrightarrow\ z=-5+2\sqrt{2}+2i\sqrt{2}\ ou\ z=-5-2\sqrt{2}-2i\sqrt{2} \end{array}$
Les solutions de l’équation sont donc $ -5+2\sqrt{2}+2i\sqrt{2} $ et $ -5-2\sqrt{2}-2i\sqrt{2} $

Exercice 9
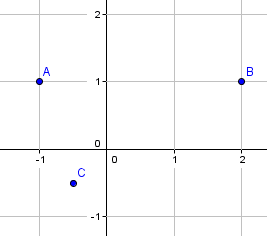
A,B et C sont les points d’affixes respectives :
$ z_A=-1+i $, $ z_B=2+i $, $ z_C=-\dfrac{1}{2}–\dfrac{1}{2}i $.
1) Placer les points A, B et C.
2) Calculer les affixes des vecteurs $ \vec{AB} $, $ \vec{AC} $ et $ \vec{BC} $.
3) En déduire les longueurs AB, AC et BC.
Le triangle ABC est-il rectangle en C?

🔻Correction Exercice 9

1)

2)
$ \begin{array}{ll}z_{\vec{AB}} &= z_B – z_A \\&= 2 + i – (-1 + i) =3 \end{array}$
$ \begin{array}{ll}z_{\vec{AC}} &= z_C – z_A \\&= -\dfrac{1}{2} – \dfrac{1}{2}i – (-1 + i) \\&=\dfrac{1}{2} – \dfrac{3}{2}i \end{array}$
$ \begin{array}{ll}z_{\vec{BC}} &= z_C – z_B \\&= -\dfrac{1}{2} – \dfrac{1}{2}i – (2 + i) \\&= -\dfrac{5}{2} – \dfrac{3}{2}i\end{array} $
3) On a donc $ AB = |3| = 3 $
$ \begin{array}{ll} AC &= \left|\dfrac{1}{2} – \dfrac{3}{2}i \right| \&= \sqrt{\dfrac{1}{4} + \dfrac{9}{4}} \\&=\sqrt{\dfrac{5}{2}} \end{array}$
$ \begin{array}{ll}BC &= \left|-\dfrac{5}{2} – \dfrac{3}{2}i \right| \\&= \sqrt{\dfrac{25}{4} + \dfrac{9}{4}} \\&=\sqrt{\dfrac{17}{2}}\end{array} $
Dans le triangle ABC, le plus grand côté est [BC].
Or $ AB^2 + AC^2 = 9 + \dfrac{5}{2} = \dfrac{23}{2}$ et $ BC^2 = \dfrac{17}{2} $.
Par conséquent $ AB^2+AC^2 \ne BC^2 $.
D’après la réciproque du théorème de Pythagore, le triangle ABC n’est pas rectangle.

Exercice 10
Dans chaque cas, trouver l’ensemble des points dont l’affixe z satisfait la condition indiquée.
1) $ |z – 3| = |z -1 + i|$
2) $ |z +2 – i| = \sqrt{5}$
3) $ |z + 3 – i| \le 2 $

🔻Correction Exercice 10

1) $ |z – 3| = |z -1 + i| \Leftrightarrow |z – 3| = |z – (1 – i)| $
On appelle M le point d’affixe $ z$, A le point d’affixe 3 et B le point d’affixe $ 1 -i$.
Par conséquent $ |z – 3| = |z – (1 – i)| \Leftrightarrow AM = BM$.
L’ensemble des points cherché est donc la médiatrice de [AB].
2) $ |z +2 – i| = \sqrt{5} \Leftrightarrow |z – (-2 + i)| = \sqrt{5}$
On appelle M le point d’affixe $ z$ et C le point d’affixe $ -2 + i$.
Par conséquent $ |z – (-2 + i)| = \sqrt{5} \Leftrightarrow CM = \sqrt{5}$.
L’ensemble des points cherché est donc le cercle de centre C et de rayon $ \sqrt{5}$.
3) $ |z + 3 – i| \le 2 \Leftrightarrow |z – (-3 +i)| \le 2$.
On appelle M le point d’affixe $ z$ et D le point d’affixe $ -3 + i$.
Par conséquent $ |z – (-3 +i)| \le 2 \Leftrightarrow DM \le 2$.
L’ensemble des points cherché est donc le disque de centre D et de rayon 2, le cercle étant inclus (il s’agit, autrement dit, du disque fermé).

Exercice 11
Quelle est la forme trigonométrique de :
$ z_1 = -1 + i \sqrt{3}$ et $ z_2 = 3-3i$?

🔻Correction Exercice 11

$ |z_1| = \sqrt{1 + 3} = 2$
Donc
$ \begin{array}{ll} z_1 &= 2\left(\dfrac{-1}{2} + \dfrac{\sqrt{3}}{2}i\right) \\&= 2\left(\cos \dfrac{2\pi}{3} + i \sin \dfrac{2\pi}{3}\right) \end{array}$
$ |z_2| = \sqrt{9 + 9} = 3\sqrt{2}$
Donc
$ \begin{array}{ll} z_2 &= 3\sqrt{2}\left(\dfrac{1}{\sqrt{2} }-\dfrac{i}{\sqrt{2}}\right) \\\\ &= 3\sqrt{2} \left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2} i\right) \\\\ & = 3\sqrt{2} \left( \cos \dfrac{-\pi}{4} + i \sin \dfrac{-\pi}{4}\right) \end{array}$

}

Exercice 12
Déterminer le module et un argument de:
1) $ z = \dfrac{1 + i}{1-i} $
2) $ z= \dfrac{1 + i \sqrt{3}}{1 + i}$
3) $ z = \dfrac{-\sqrt{2}}{1 + i}$

🔻Correction Exercice 12

1) $ |1 + i| = \sqrt{1 + 1} = \sqrt{2}$
$ \begin{array}{ll} 1 + i &= \sqrt{2} \left( \dfrac{1}{\sqrt{2}} + \dfrac{i}{\sqrt{2}} \right) \\&= \sqrt{2} \left(\cos \dfrac{\pi}{4} + i \sin \dfrac{\pi}{4}\right) \end{array}$
Par conséquent $ arg(1 + i) = \dfrac{\pi}{4} [2\pi] $
$ |1 – i| = \sqrt{1 + 1} = \sqrt{2}$.
$ \begin{array}{ll} 1 – i &= \sqrt{2} \left( \dfrac{1}{\sqrt{2}}-\dfrac{i}{\sqrt{2}} \right) \\&= \sqrt{2} \left(\cos \dfrac{-\pi}{4} + i \sin \dfrac{-\pi}{4}\right) \end{array}$
4) Par conséquent $ arg(1-i) = -\dfrac{\pi}{4} [2\pi] $
Donc $ |z| = \dfrac{\sqrt{2}}{\sqrt{2}} = 1$
Et $ arg(z) = \dfrac{\pi}{4}-\dfrac{-\pi}{4} = \dfrac{\pi}{2} [2\pi] $
On pouvait également déterminer la forme algébrique de $z$
(on obtient $ i$) et ensuite déterminer le module et un argument.
2) $ \left| 1 + i\sqrt{3}\right| = 2$
$ \begin{array}{ll} 1 + i \sqrt{3} &= 2\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i \right) \\&= 2\left( \cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right) \end{array}$
Par conséquent $ arg\left(1 + i \sqrt{3}\right) = \dfrac{\pi}{3} [2\pi] $.
$ |1 + i| = \sqrt{1 + 1} = \sqrt{2}$
$ \begin{array}{ll} 1 + i &= \sqrt{2} \left( \dfrac{1}{\sqrt{2}} + \dfrac{i}{\sqrt{2}} \right) \\ &= \sqrt{2} \left(\cos \dfrac{\pi}{4} + i \sin \dfrac{\pi}{4}\right) \end{array}$
Par conséquent $ arg(1 + i) = \dfrac{\pi}{4} [2\pi] $
Donc $ |z| = \dfrac{2}{\sqrt{2}} = \sqrt{2}$
Et $ arg(z) = \dfrac{\pi}{3} – \dfrac{\pi}{4} = \dfrac{\pi}{12} [2\pi] $.
3) $ -\sqrt{2} = \sqrt{2}\left(\cos \pi + i \sin \pi\right) $ C’est un réel négatif !
Donc $ arg\left(-\sqrt{2} \right) = \pi [2\pi] $.
$ |1 + i| = \sqrt{1 + 1} = \sqrt{2}$
$ \begin{array}{ll} 1 + i &= \sqrt{2} \left( \dfrac{1}{\sqrt{2}} + \dfrac{i}{\sqrt{2}} \right) \\&= \sqrt{2} \left(\cos \dfrac{\pi}{4} + i \sin \dfrac{\pi}{4}\right) \end{array}$
Par conséquent $ arg(1 + i) = \dfrac{\pi}{4} [2\pi] $
Donc $ |z| = \dfrac{\sqrt{2}}{\sqrt{2}} = 1$
Et $ arg(z) = \pi – \dfrac{\pi}{4} = \dfrac{3\pi}{4} [2\pi] $.

Exercice 13
Mettre chaque nombre complexe sous forme trigonométrique.
1) $ z = (-1 + i)^5$
2) $ z = \left(\sqrt{3}-i\right)^4$
3) $ z = \dfrac{\left(\sqrt{2}-1\right)i}{1 – i}$

🔻Correction Exercice 13

1) $ |- 1 + i| = \sqrt{2}$
Donc
$ \begin{array}{ll} -1 + i &= \sqrt{2} \left(-\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2}\right) \\&= \sqrt{2}\left(\cos \dfrac{3\pi}{4} + i \sin \dfrac{3\pi}{4}\right). \end{array}$
Donc $ arg(-1 + i) = \dfrac{3\pi}{4} [2\pi] $.
Par conséquent
$ arg\left((-1 + i)^5\right) = 5 \times \dfrac{3\pi}{4} [2\pi]= -\dfrac{\pi}{4} [2\pi] $
Ainsi
$ \begin{array}{ll} (-1 + i)^5 &= \sqrt{2}^5\left(\cos \dfrac{-\pi}{4}+i \sin \dfrac{-\pi}{4}\right) \\\\ &= 4\sqrt{2}\left(\cos \dfrac{-\pi}{4}+i \sin \dfrac{-\pi}{4}\right) \end{array}$
2) $ \left|\sqrt{3}-i \right| = 2$.
$ \begin{array}{ll} \sqrt{3}-i &= 2 \left(\dfrac{\sqrt{3}}{2}-\dfrac{i}{2}\right) \\&= 2\left(\cos \dfrac{-\pi}{6} + i \sin \dfrac{-\pi}{6}\right) \end{array}$
Donc $ arg\left(\sqrt{3}-i\right) = -\dfrac{\pi}{6} [2\pi] $.
Par conséquent
$ arg\left(\left(\sqrt{3}-i\right)^4\right) = 4 \times \dfrac{-\pi}{6} = -\dfrac{2\pi}{3} [2\pi] $.
Ainsi
$ \begin{array}{ll} \left(\sqrt{3} – i\right)^4 &= 2^4\left(\cos \dfrac{-2\pi}{3} + i \sin \dfrac{-2\pi}{3} \right) \\\\ & = 16\left(\cos \dfrac{-2\pi}{3} + i \sin \dfrac{-2\pi}{3} \right) \end{array}$
$ \left|\left(\sqrt{2}-1\right)i\right| = \sqrt{2}-1 arg\left(\left(\sqrt{2}-1\right)i\right) = \dfrac{\pi}{2}$.
$ |1-i| = \sqrt{2}$
$ \begin{array}{ll} 1-i& = \sqrt{2}\left(\dfrac{1}{\sqrt{2}}-\dfrac{i}{\sqrt{2}}\right)\\& = \sqrt{2}\left(\cos \dfrac{-\pi}{4}+i \sin \dfrac{-\pi}{4}\right) \end{array}$
Donc $ arg (1-i) = -\dfrac{-\pi}{4}$
Ainsi $ |z| = \dfrac{\sqrt{2}-1}{\sqrt{2}}$
Et $ arg(z) = \dfrac{\pi}{2}-\dfrac{-\pi}{4} = \dfrac{3\pi}{4}$
Donc
$ z = \dfrac{\sqrt{2}-1}{\sqrt{2}}\left(\cos \dfrac{3\pi}{4} + i \sin \dfrac{3\pi}{4} \right) $

Exercice 14
Écrire sous forme trigonométrique chacun des nombres complexes suivants :
1) $ z = \left(\sin \dfrac{\pi}{6} + i \cos \dfrac{\pi}{6}\right)^6$
2) $ arg(i z) = \dfrac{3\pi}{4} [2\pi]et |z| = 2$

🔻Correction Exercice 14

1) On a
$ \begin{array}{ll} z &= \left(\sin \dfrac{\pi}{6} + i \cos \dfrac{\pi}{6}\right)^6 \\\\ & = \left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i\right)^6 \\\\ & = \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)^6 \end{array}$
Par conséquent $ arg(z) = 6 \times \dfrac{\pi}{3} = 2\pi [2\pi] = 0 [2\pi] $.
Donc $ z = \cos 0 + i \sin 0$ .
2) On a
$ \begin{array}{ll} arg(i z) = \dfrac{3\pi}{4} [2\pi] &\Leftrightarrow arg(i) + arg(z) = \dfrac{3\pi}{4} [2\pi] \\ &\Leftrightarrow \dfrac{\pi}{2} + arg(z) = \dfrac{3\pi}{4} [2\pi] \\&\Leftrightarrow arg(z) = \dfrac{\pi}{4} [2\pi] . \end{array}$
Donc $ z = 2\left(\cos \dfrac{\pi}{4} + i \sin\dfrac{\pi}{4}\right) $.

Exercice 15
On donne les nombres complexes :
$ z_1 = \dfrac{\sqrt{6}-i \sqrt{2}}{2}$ et $ z_2 = 1-i$.
1) Donner une forme trigonométrique de $ z_1$, $ z_2$ et $ \dfrac{z_1}{z_2}$.
2) Donner la forme algébrique de $ \dfrac{z_1}{z_2}$.
3) En déduire la forme exacte de $ \cos \dfrac{\pi}{12}$ et de $ \sin \dfrac{\pi}{12}$.

🔻Correction Exercice 15

1) $ |z_1| = \dfrac{\sqrt{6 + 2}}{2} = \sqrt{2}$
Donc
$ \begin{array}{ll} z_1 &= \sqrt{2} \left(\dfrac{\sqrt{3}}{2}-\dfrac{i}{2} \right) \\&= \sqrt{2} \left(\cos \dfrac{-\pi}{6} + i \sin \dfrac{-\pi}{6}\right)\end{array} $
$ |z_2| = 2$
donc
$ \begin{array}{ll} z_2 &= 2\left(\dfrac{1}{2}-\dfrac{i}{2}\right) \\&= 2\left(\cos \dfrac{-\pi}{4} + i \sin \dfrac{-\pi}{4}\right) \end{array}$
Par conséquent
$ arg\left(\dfrac{z_1}{z_2}\right) = \dfrac{-\pi}{6}-\dfrac{-\pi}{4} = \dfrac{\pi}{12} [2\pi] $ .
Et $ \left|\dfrac{z_1}{z_2}\right| = \dfrac{\sqrt{2}}{\sqrt{2}} = 1$.
Ainsi $\dfrac{z_1}{z_2} = \cos \dfrac{\pi}{12} + i \sin \dfrac{\pi}{12}$
2) On a
$ \begin{array}{ll} \dfrac{z_1}{z_2} &= \dfrac{\dfrac{\sqrt{6} – i \sqrt{2}}{2}}{1 – i} \\\\ & = \dfrac{\sqrt{6}-i \sqrt{2}}{2(1-i)} \times \dfrac{1 + i}{1 + i} \\\\ & = \dfrac{\sqrt{6} + i \sqrt{6}-i \sqrt{2} + \sqrt{2}}{4} \\\\ &= \dfrac{\sqrt{6} + \sqrt{2}}{4} + \dfrac{\sqrt{6}-\sqrt{2}}{4} i \end{array}$
3) En identifiant les formes trigonométriques et algébriques de $\dfrac{z_1}{z_2}$ on obtient :
$ \cos \dfrac{\pi}{12} = \dfrac{\sqrt{6} + \sqrt{2}}{4}$ et $ \sin \dfrac{\pi}{12} = \dfrac{\sqrt{6}-\sqrt{2}}{4}$

Exercice 16
On rappelle les formules trigonométriques :
$ \cos(2a) = 2\cos^2 a-1 $ et $ \sin(2a) = 2 \sin a \cos a$
On note $ z_1 = 1 + \cos \alpha + i \sin \alpha$ avec $\alpha \in[0;\pi[$.
1) Démontrer que $ z_1= 2\cos \dfrac{\alpha}{2} \left(\cos \dfrac{\alpha}{2} + i \sin \dfrac{\alpha}{2}\right) $.
2) En déduire le module et un argument de $ z_1$.
3) Reprendre la question précédente lorsque $ \alpha \in ]\pi;2\pi] $.

🔻Correction Exercice 16

1) On a
$ \begin{array}{ll} z_1 & = 1 + \cos \dfrac{2 \alpha}{2} + i \sin \dfrac{2\alpha}{2} \\\\ & = 2\cos^2 \dfrac{\alpha}{2} + 2i \sin \dfrac{\alpha}{2} \cos \dfrac{\alpha}{2} \\\\ & = 2\cos \dfrac{\alpha}{2} \left(\cos \dfrac{\alpha}{2} + i \sin \dfrac{\alpha}{2}\right) \end{array}$
2) $ \alpha \in [0;\pi[ donc \dfrac{\alpha}{2} \in \left[0;\dfrac{\pi}{2}\right[$
Par conséquent
$ \cos \dfrac{\alpha}{2} > 0$ et $ \sin \dfrac{\alpha}{2} \ge 0$
On a donc fournit la forme trigonométrique de $ z_1$.
Ainsi $\left|z_1 \right| =2\cos \dfrac{\alpha}{2}$ et $arg(z_1) = \dfrac{\alpha}{2} [2\pi] $ .
3) $\alpha \in ]\pi;2\pi] $ donc $\dfrac{\alpha}{2} \in ]\dfrac{\pi}{2};\pi] $
Par conséquent $\cos \dfrac{\alpha}{2} < 0$ et $\sin \dfrac{\alpha}{2} \ge 0$
Ainsi, l’expression de $z_1$ n’est donc pas donnée sous sa forme trigonométrique.
$\begin{array}{ll} z_1 &= -2\cos \dfrac{\alpha}{2} \left(-\cos \dfrac{\alpha}{2} – i \sin \dfrac{\alpha}{2}\right) \\\\ &= -2\cos \dfrac{\alpha}{2} \left(\cos \left(\pi + \dfrac{\alpha}{2}\right) + i \sin \left(\pi + \dfrac{\alpha}{2}\right)\right) \end{array}$
Donc $\left|z_1\right| = -2\cos \dfrac{\alpha}{2}$ et $arg\left(z_1\right) = \pi + \dfrac{\alpha}{2} [2\pi] $

Exercice 17
On considère le polynôme $P(z)=z^4-2z^3-2z-1$.
1) Calculer $P(i) $ et $P(-i) $.
2) En déduire que $P(z)=\left(z^2+1\right)\left(az^2+bz+c\right) $ où $a$, $b$ et $c$ sont des réels qu’on déterminera.
3) En déduire la résolution de l’équation $P(z)=0$ dans $\mathbb{C}$.

🔻Correction Exercice 17

1) $P(i) = i^4-2i^3-2i -1 = 1 +2i-2i-1 = 0$.
$P(-i)=(-i)^4-2(-i)^3-2(-i)-1 = 1-2i+2i-1=0$.
2) Il existe donc trois réels $a$, $b$ et $c$ tels que : $P(z)=(z-i)(z+i)\left(az^2+bz+c\right) $
Soit
$\begin{array}{ll} P(z) &= \left(z^2+1\right)\left(az^2+bz+c\right) &=az^4+bz^3+cz^2+az^2+bz+c &=az^4+bz^3+(a+c)z^2+bz+c \end{array}$
On identifie avec le polynôme initial. On trouve alors :
$\begin{cases} a=1 \\b=-2a+c=0 \\b=-2c=-1 \end{cases} $ $\Leftrightarrow \begin{cases} a=1\\b=-2\\c=-1\end{cases}$
Par conséquent $P(z)=\left(z^2+1\right)\left(z^2-2z-1\right) $.
3) Résolvons l’équation $z^2-2z-1=0$.
$\Delta = (-2)^2-4\times 1 \times (-1) = 8 >0$
Il y a donc deux racines réelles
$z_1=\dfrac{2-\sqrt{8}}{2}=1-\sqrt{2}$ et $z_2=1+\sqrt{2}$.
Ainsi
$\begin{array}{ll} P(z)=0 &\Leftrightarrow \left(z^2+1\right)\left(z^2-2z-1\right) = 0 \\&\Leftrightarrow z^2+1=0 \text{ ou } z^2-2z-1=0 \\&\Leftrightarrow z \in \left\{i,-i,1-\sqrt{8},1+\sqrt{8}\right\} \end{array}$
Les solutions de l’équation $P(z)=0 $ sont donc $ i,-i, 1-\sqrt{8},1+\sqrt{8}$.
$z_1=\dfrac{2-\sqrt{8}}{2}=1-\sqrt{2}$ et $ z_2=1+\sqrt{2}$.

Exercice 18
Déterminer l’ensemble des points $M(z) $ du plan complexe tels que $\dfrac{z+1}{z-i}$ soit
1) un imaginaire pur
2) un réel

🔻Correction Exercice 18

On note $z=x+i y$. Pour tout complexe $z\neq i $ on a :
$\begin{array}{ll} \dfrac{z+1}{z-i} &= \dfrac{x+i y +1}{x+i y – i} \\&= \dfrac{x+1+i y}{x + i(y-1) } \\&= \dfrac{x+1+i y}{x + i (y-1)} \times \dfrac{x – i(y-1)}{x – i(y-1)} \\&=\dfrac{x(x+1)+y(y-1)+i\left(yx-(x+1)(y-1)\right)}{x^2+(y-1)^2} \\&=\dfrac{x^2+x+y^2-y+i (yx-xy+x-y+1)}{x^2+(y-1)^2} \\&=\dfrac{x^2+x+y^2-y+i (x-y+1)}{x^2+(y-1)^2} \end{array}$
1) On a
$\begin{array}{ll}\dfrac{z+1}{z-i} \text{ est un imaginaire pur} &\Leftrightarrow \dfrac{x^2+x+y^2-y}{x^2+(y-1)^2}=0 \\&\Leftrightarrow x^2+x+y^2-y=0 \text{ et } x^2+(y-1)^2\neq 0 \\&\Leftrightarrow \left(x+\dfrac{1}{2}\right)^2-\dfrac{1}{4}+\left(y-\dfrac{1}{2}\right)^2-\dfrac{1}{4} = 0 \text{ et } (x;y)\neq(0;1) \\&\Leftrightarrow \left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2= \dfrac{1}{2} \text{ et } (x;y)\neq(0;1) \end{array}$
Donc l’ensemble des points cherché est le cercle de centre $A\left(-\dfrac{1}{2}+\dfrac{i}{2}\right)$ et de rayon $\sqrt{\dfrac{1}{2}} = \dfrac{\sqrt{2}}{2}$ privé du point d’affixe $i$.
2) On a
$\begin{array}{ll} \dfrac{z+1}{z-i} est un réel &\Leftrightarrow \dfrac{x-y+1}{x^2+(y-1)^2}=0 \\&\Leftrightarrow x-y+1=0 \text{ et } (x;y)\neq (0;1) \end{array}$
Donc l’ensemble des points cherché est la droite d’équation $x-y+1=0$ privée du point d’affixe $ i$.

Exercice 19
Les deux questions sont indépendantes
1) Déterminer et représenter l’ensemble des points $M(z) $ du plan complexe tels que $|z|=\left|\dfrac{2+i}{z}\right| = |z-1|$.
2) Déterminer et représenter l’ensemble des points $M(z) $ du plan complexe tels que $|z|=2|z-i|$.

🔻Correction Exercice 19

1) On cherche donc l’ensemble des points qui vérifient à la fois $|z|=\left|\dfrac{2+i}{z}\right|$ et $|z|=|z-1|$.
$\begin{array}{ll} |z|=\left|\dfrac{2+i}{z}\right| &\Leftrightarrow |z|^2=|2+i| \\&\Leftrightarrow |z|^2=\sqrt{5} \\&\Leftrightarrow |z|=\sqrt{\sqrt{5}} \end{array}$
L’ensemble des points vérifiant $|z|=\left|\dfrac{2+i}{z}\right|$ est le cercle de centre O, l’origine du repère, et de rayon $\sqrt{\sqrt{5}}$.
Si on appelle M le point d’affixe z, A le point d’affixe 1 alors $|z|=|z-1| \Leftrightarrow OM=AM$.
L’ensemble des points vérifiant $|z|=|z-1| $ est donc la médiatrice du segment [0A].
L’ensemble des points cherché est donc l’intersection du cercle et de la droite, c’est-à-dire les points B et C.

On note $z=x+i y$.
$\begin{array}{ll} |z|=2|z-i\| &\Leftrightarrow |z|^2=4|z-i|^2 \\&\Leftrightarrow x^2+y^2=4\left|x+i y – i\right|^2 \\&\Leftrightarrow x^2+y^2=4\left(x^2+(y-1)^2\right) \\&\Leftrightarrow x^2+y^2=4(x^2+y^2-2y+1) \\&\Leftrightarrow 0=3x^2+3y^2-8y+4 \\&\Leftrightarrow x^2+y^2-\dfrac{8}{3}y+\dfrac{4}{3}=0 \\&\Leftrightarrow x^2+\left(y-\dfrac{4}{3}\right)^2-\dfrac{16}{9}+\dfrac{4}{3} =0 \\&\Leftrightarrow x^2+\left(y-\dfrac{4}{3}\right)^2 = \dfrac{4}{9} \end{array}$
L’ensemble des points cherché est donc le cercle de centre le point A d’affixe $\dfrac{4}{3}i$ et de rayon $\sqrt{\dfrac{4}{9}}=\dfrac{2}{3}$.

Exercice 20
Pour tout nombre complexe z différent de -1, montrer que :
$\dfrac{z^2}{z+1}\in \mathbb{R} \Leftrightarrow z=\overline{z} \ ou\ \overline{z}z+z+\overline{z}=0$.

🔻Correction Exercice 20

On note $z=x+i y$.
$\begin{array}{ll} &\dfrac{z^2}{z+1} \\&=\dfrac{(x^+i y)^2}{x+i y+1} \\&=\dfrac{x^2-y^2+2i xy}{(x+1)+i y} \times \dfrac{(x+1)-i y}{(x+1)-i y} \\&=\dfrac{\left(x^2-y^2\right)(x+1)+2xy^2-\left(x^2-y^2\right)i y + 2i xy(x+1)}{(x+1)+y^2} \\&=\dfrac{\left(x^2-y^2\right)(x+1)+2xy^2+i \left(-\left(x^2-y^2\right)y + 2 xy(x+1)\right)}{(x+1)^2+y^2} \end{array}$
Or
$\begin{array}{ll} &\dfrac{z^2}{z+1}\in \mathbb{R} \\&\Leftrightarrow \Im\text{m}\left(\dfrac{z^2}{z+1}\right) = 0 \\& \Leftrightarrow \dfrac{-\left(x^2-y^2\right)y + 2 xy(x+1)}{(x+1)^2+y^2} =0 \\& \Leftrightarrow y\left(-\left(x^2-y^2\right) + 2 x(x+1)\right) = 0 \text{ et } (x+1)^2+y^2\neq 0 \\& \Leftrightarrow y\left(-x^2+y^2+2x^2+2x\right)=0 \text{ et } (x;y)\neq (-1;0) \\& \Leftrightarrow y\left(x^2+y^2+2x\right)=0 \text{ et } (x;y) \neq (-1;0) \\& \Leftrightarrow \left(y=0 \text{ ou } x^2+y^2+2x=0\right) \text {et } (x;y) \neq (-1;0) \end{array}$
Mais $y=0 \Leftrightarrow z=\overline{z}$ et
$\overline{z}z+z+\overline{z} = x^2+y^2+x+i y+ x-iy = x^2+y^2+2x$.
Par conséquent, pour tout nombre complexe z différent de -1 :
$ \dfrac{z^2}{z+1}\in \mathbb{R} \\ \Leftrightarrow z=\overline{z} \text{ ou } \overline{z}z+z+\overline{z}=0$.

Exercice 21
1) Déterminer l’ensemble des points M du plan complexe dont l’affixe $z_M$ vérifie : $\left|z_M-i +1\right|=3$.
2) Déterminer l’ensemble des points M du plan complexe dont l’affixe $z_M$ vérifie : $\left|z_M-i+1\right|=\left|z_M-i\right|$.

🔻Correction Exercice 21

1) On a:
$\begin{array}{ll} |z_M-i+1|=3 &\Leftrightarrow |z_M-(-1+i)|=3 \\&\Leftrightarrow AM=3 \ avec\ A(-1+i).\end{array}$
L’ensemble cherché est donc le cercle de centre $A(-1+i) $ et de rayon 3.
2) On a:
$\begin{array}{ll} |z_M-i+1|=|z_M-i| &\Leftrightarrow |z_M-(-1+i)|=\left|z_M-i\right| \\&\Leftrightarrow AM=BM \ avec\ A(-1+i) \ et\ B(i).\end{array}$
L’ensemble cherché est donc la médiatrice du segment [AB] avec $A(-1+i) $ et $B(i) $.

Exercice 22
Dans le plan complexe rapporté au repère orthonormé direct $ (O ; \vec{e_1}, \vec{e_2})$, on considère les points A , B et C d'affixes respectives $a=1$, $b=1+2 i$ et $c=1+\sqrt{3}+i $
Calculer $ \large{\frac{c-a}{b-a}}$ et l'écrire sous la forme exponentielle.
En déduire la nature du triangle ABC.

🔻Correction Exercice 22

A, B et C ayant pour affixes respectives $a=1$, $b=1+2i$ et $c=1+\sqrt{3}+i$
$\begin{array}{ll} \large{\frac{c-a}{b-a}} &=\large{\frac{1+\sqrt{3}+i-1}{1+2 i-1}} \\&=\large{\frac{\sqrt{3}+i}{2 i}} \\&=\large{\frac{(\sqrt{3}+i)i}{2 i^{2}}} \\&=\large{\frac{-1+i \sqrt{3}}{-2}} \\&=\large{\frac{1}{2}-i \frac{\sqrt{3}}{2}} \end{array}$
donc $\large{\frac{c-a}{b-a}=e^{-i \frac{\pi}{3}}} $
On sait que $\large{ \frac{ AC }{ AB }}=\left|\frac{c-a}{b-a}\right|$ donc $\frac{ AC }{ AB }=\left|e^{-i \frac{\pi}{3}}\right|=1$
Donc AC = AB et $\overline{(\vec{AB}, \vec{AC}) }=\arg \left(\frac{c-a}{b-a}\right)[2 \pi] $
Donc $\overline{(\vec{AB}, \vec{AC}) }=\arg \left(e^{-i \frac{\pi}{3}}\right)=-\frac{\pi}{3}[2 \pi] $

Exercice 23
1) Résoudre dans $\mathbb{C}$ l'équation $z^{2}-2z+5=0$
2) Le plan complexe est rapporté à un repère orthonormé direct $ (O ; \vec{e_1}, \vec{e_2})$ d'unité graphique 2 cm.
On considère les points A, B, C et D d'affixes respectives:
$z_A=1+2i $ ; $z_B=\overline{z_A}$ ; $z_C=1+\sqrt{3}+i$ ; $ z_D= \overline{z_C }$
a) Placer les points A et B dans le repère $ (O ; \vec{e_1}, \vec{e_2})$.
b) Calculer $\frac{z_B-z_C}{z_A-z_C}$ et donner le résultat sous forme algébrique.
En déduire la nature du triangle ABC.
3) Démontrer que A, B, C et D appartiennent à un même cercle $\Gamma$ dont on précisera le centre et le rayon.
4) Construire les points C et D dans le repère $ (O ; \vec{e_1}, \vec{e_2})$ .
Expliquer la construction proposée.

🔻Correction Exercice 23

1) L'équation $z^{2}-2 z+5=0$ est une équation du second degré à coefficients réels.
Elle a pour discriminant $\Delta=(-2)^{2}-4 \times 1\times 5=4-20=-16=(4i)^{2}$
On en déduit ses deux solutions:
$z_1=\frac{-(-2)-4i}{2 \times 1}= \frac{2-4i}{2}=1-2i$ et $z_2=\frac{-(-2)+4i}{2 \times 1}=\frac{2+4i}{2}=1+2 i $
L'équation $z^{2}-2z+5=0$ a pour solutions $1-2 i$ et $1+2 i $
2) a) On place le point A d'affixe $z_A=1+2i$ et le point B d'afffixe $z_B=\overline{z_A}=1-2i $
Comme $z_B =\overline{z_A}$ les points A et B sont symétriques par rapport à l'axe $ ( O ; \vec{e_1 } ) $
Voir graphique ci-dessous.
b) On a:
$\begin{array}{ll} \normalsize{\dfrac{z_B-z_C}{z_A-z_C} }&= \large{\frac{1-2i-1-\sqrt{3}-i}{1+2i-1-\sqrt{3}-i}} \\&=\large{\frac{-\sqrt{3}-3i}{-\sqrt{3}+i}} \\&=\large{\frac{(-\sqrt{3}-3 i)(-\sqrt{3}-i)}{(-\sqrt{3}+i)(-\sqrt{3}-i)}} \\&=\large{\frac{3+i \sqrt{3}+3i \sqrt{3}-3}{3+1}} \\&=\large{\frac{4 i \sqrt{3}}{4}} \end{array}$
Donc $ \frac{z_B-z_C}{z_A-z_C}=i \sqrt{3}$
On a $\arg \frac{z_B-z_C}{z_A-z_C}=\arg (i \sqrt{3})=\frac{\pi}{2}[2 \pi] $, c'est-à-dire que: $\overline{ (\vec{CA} ; \vec{CB})}=\frac{\pi}{2}[2 \pi] $
Donc le triangle ABC est rectangle en C.
NB : Ce triangle n'est pas isocèle car
$\left|\frac{z_B-z_C}{z_A-z_C}\right|=|i \sqrt{3}|=\sqrt{3} $ donc $BC=\sqrt{3} AC$
3) Le triangle ABC étant rectangle en C, les points A, B et C sont sur le cercle $\Gamma$ de diamètre [AB]
Le milieu de [ AB] est sur l'axe $ ( O ; \vec{e_1}) $ puisque A et B sont symétriques par rapport à $ ( O ; \vec{e_1})$
Le cercle $\Gamma $ est donc symétrique par rapport à $ (O ; \vec{e_1})$
Sachant que $ z_D=\overline{z_C}$, les points C et D sont symétriques par rapport à $ ( O ; \vec{e_1}) $
Donc le point D est aussi sur le cercle $\Gamma$
On a $AB=\left|z_B-z_A\right|=|1-2i-1-2i|=|-4i|=4$
Donc $\frac{AB}{2}=2$ et le milieu $I $ de [AB] a pour affixe $\frac{1-2i+1+2i}{2}=1$
A, B , C et D appartiennent au cercle $\Gamma$ de centre $I$ d'affixe 1 et de rayon 2
4) On peut construire le cercle $\Gamma $
On sait que le point C a pour affixe $1+\sqrt{3}+i $
donc son ordonnée est 1 et son abscisse est $1+\sqrt{3}$ elle est supérieure à 1
C est le point d'intersection du cercle $\Gamma $ et de la droite d'équation $y=1$ dont l'abscisse est supérieure à 1
D est le symétrique de C par rapport à l'axe des abscisses.

Exercice 24
Déterminer la traduction complexe de la transformation $f $ dans chacun des cas suivants:
1) $f $ est la translation de vecteur $\vec{u}(-5 ; 2) $
2) $f $ est I'homothétie de rapport $\frac{-1}{2} $ et de centre $\Omega(-4+i) $
3) $f$ est la rotation d’angle $\frac{3 \pi}{4}$ et de centre 0
4) $f$ est la rotation d’angle $\frac{4 \pi}{3}$ et de centre $\Omega(-4+i) $

🔻Correction Exercice 24

1) La traduction complexe de la translation f de vecteur $ \vec{u}(-5 ; 2) $ est: $z^{\prime}=z-5+2 i$
2) La traduction complexe de l'homothétie $f$ de rapport $\frac{-1}{2}$ et de centre $\Omega(-4+i) $ est :
$\begin{array}{ll} z^{\prime}&=-\frac{1}{2}[z-(-4+i)]+(-4+i) \\&=-\frac{1}{2} z-6+i \frac{3}{2}\end{array}$
3) La traduction complexe de la rotation $f $ d'angle $ \frac{3 \pi}{4}$ et de centre O est: $z^{\prime}=e^{3 i \pi / 4} z $
4) La traduction complexe de la rotation $f$ d'angle $\frac{4 \pi}{3}$ et de centre $\Omega(-4+i) $ est:
$z^{\prime}=e^{4 i \pi / 3}(z+4-i)-4+i $

Exercice 25
On considère les points $A(1+ i) $ et $B(-1+ 2i) $.
1) Déterminer l'affixe de C tel que le quadrilatère OACB soit un parallélogramme.
2) Déterminer l'affixe du point D, image de C par la rotation de centre B et d'angle $\dfrac{\pi}{6}$ .
3) Déterminer l'affixe du point E antécédent de C par la rotation de centre A et d'angle $-\dfrac{\pi}{6}$.
4) Démontrer que D est l'image de E par la rotation de centre O et d'angle $\dfrac{\pi}{6}$.
En déduire la nature du triangle ODE.

🔻Correction Exercice 25

On considère les points $A(1+ i) $ et $B(-1 + 2i) $.
1) Le quadrilatère OACB est un parallélogramme si et seulement si $\vec{OA}=\vec{BC}$ .
En termes complexes, cela se traduit par :
$\begin{array}{ll} \vec{OA}=\vec{BC} &\Leftrightarrow z_\vec{OA}=z_\vec{BC} \\&\Leftrightarrow z_A=z_C-z_B \\&\Leftrightarrow z_C=3i \end{array}$
Donc, le quadrilatère OACB est un parallélogramme si et seulement si l'affixe du point C est $3i$.

2) La traduction complexe de la rotation de centre B et d'angle $\dfrac{\pi}{6}$ est :
$z’=e^{i \tiny{\dfrac{\pi}{6}}}(z-z_B)+z_B$
Soit: $z’=e^{i \tiny{\dfrac{\pi}{6}}}(z+1-2i)-1+2i$
Comme D est l'image de C, on obtient facilement maintenant l'affixe de D :
$\begin{array}{ll} z_D&=(\dfrac{\sqrt{3}}{2}+i \dfrac{1}{2})(1+i)-1+2i \\&=\dfrac{\sqrt{3}-3}{2}+i \dfrac{\sqrt{3}+5}{2} \end{array}$
L'affixe du point D est donc :
$z_D=\dfrac{\sqrt{3}-3}{2}+i \dfrac{\sqrt{3}+5}{2}$
3) E est l'antécédent de C par la rotation de centre A et d'angle $\dfrac{\pi}{6}$ si et seulement si E est l'image de C par la rotation de centre A et d'angle $-\dfrac{\pi}{6}$ .
Eh oui, c'est la rotation inverse.
La traduction complexe de la rotation de centre A et l'angle $-\dfrac{\pi}{6}$ est la suivante:
$z’=e^{-i\tiny{\dfrac{\pi}{6}}}(z-z_A)+z_A$
Soit : $z’=e^{-i \tiny{\dfrac{\pi}{6}}}(z-1-i)+1+i $
On obtient donc facilement l'affixe du point E :
$\begin{array}{ll} z_E&=(\dfrac{\sqrt{3}}{2} - i \dfrac{1}{2})(2i-1)+1+i\\&=-\dfrac{\sqrt{3}}{2}+2+i (\sqrt{3}+\dfrac{3}{2})\end{array}$
L'affixe du point E est donc la suivante :
$z_E =-\dfrac{\sqrt{3}}{2}+2+i (\sqrt{3}+\dfrac{3}{2}) $
4) La tradcution complexe de la rotation de centre O et d'angle $\dfrac{\pi}{6}$ est : $ z’=e^{i \tiny{\dfrac{\pi}{6}}}z$
L'image de E par cette rotation a pour affixe :
$e^{i \tiny{\dfrac{\pi}{6}}} z_E=(\dfrac{\sqrt{3}}{2} +i \dfrac{1}{2})[-\dfrac{\sqrt{3}}{2}+2+i (\sqrt{3}+\dfrac{3}{2})]$
$e^{i \tiny{\dfrac{\pi}{6}}} z_E =-\dfrac{3}{4} +\sqrt{3} -\dfrac{1}{2} (\sqrt{3}+\dfrac{1}{2})+i(-\dfrac{\sqrt{3}}{4}+1+\dfrac{{3}}{2}+\dfrac{3\sqrt{3}}{4})$
$e^{i \tiny{\dfrac{\pi}{6}}} z_E =-\dfrac{\sqrt{3}-3}{2}+i \dfrac{\sqrt{3}+5}{2}$
Soit en fait : $e^{i \tiny{\dfrac{\pi}{6}}} z_E =z_D$
Donc, les rotations sont des isométries.
On en déduit que OE = OD et donc que ODE est isocèle.

Exercice 26
Déterminer la nature et les éléments caractéristiques de la transformation f qui à tout point M d'affixe z associe le point M’ d’affixe z’ tel que :
1) $z'= z+2-3i$
2) $z'= -4 z+2-3i$
3) $z'=i z+2+i$
4) $z'=\frac{-1+i \sqrt{3}}{2} z+2-i$

🔻Correction Exercice 26

1) $ z'=z+2-3i$
C'est du cours, f est la translation de vecteur d'afflixe $2-3 i $
2) $ z’=-4 z+2 - 3i$.
Ici, $f$ est l'homothétie de rapport -4 et de centre $\Omega$ d'affixe $\omega$ est un point invariant par $f$, donc:
$\begin{array}{ll}\omega=-4 \omega+2-3i &\Leftrightarrow \omega+4 \omega=2-3i \\&\Leftrightarrow \omega =\frac{2}{5}-\frac{3}{5} i\end{array}$
3) $ z’=i z+2+i$
est la rotation d'angle $arg(i)=\frac{\pi}{2}$ et centre $\Omega$ d'aftixe $\omega$ est un point invariant par $f$, donc:
$\begin{array}{ll} \omega=i \omega+2+i&\Leftrightarrow \omega-i \omega=2+i \\&\Leftrightarrow \omega =\frac{2+i}{1-i}=\frac{(2+i)(1+i)}{2}=\frac{1}{2}+\frac{3}{2} I \end{array} $
4) $z’=\frac{-1+i \sqrt{3}}{2} z+2-i$
on a : $| \frac{-1+i \sqrt{3}}{2} |=1$
Et: $\frac{-1+i \sqrt{3}}{2} \neq 1$
Donc $f $ est la rotation de centre $\Omega$ d'affixe $\omega $ et d'angle : $\arg \left(\frac{-1+I \sqrt{3}}{2}\right)=\frac{2 \pi}{3}$
$\Omega$ est un point invariant par $f$, donc:
$\begin{array}{ll} \omega=\frac{-1+i \sqrt{3}}{2} \omega+2-i &\Leftrightarrow 2\omega=(-1+i \sqrt{3}) \omega + 2(2-i ) \\&\Leftrightarrow 2\omega-(-1+i \sqrt{3}) \omega = 2(2-i ) \\&\Leftrightarrow \omega =\frac{2(2-1)}{3-I \sqrt{3}} =1+\frac{\sqrt{3}}{6}+i\left(\frac{\sqrt{3}}{3}-\frac{1}{2}\right) \end{array}$
Du coup, $f $ est la rotation d'angle $\frac{2 \pi}{3}$ et de centre $\Omega$ d'affixe : $1+\frac{\sqrt{3}}{6}+i\left(\frac{\sqrt{3}}{3}-\frac{1}{2}\right) $

Exercice 27
Le plan complexe est muni d’un repère orthonormé direct $ (O;\vec{i},\vec{j})$. On note A le point d’affixe $i$.
À tout point M du plan, distinct de A, d’affixe z, on associe le point M’ d’affixe $z’ = \dfrac{i z}{z – i}$.
1. a. Déterminer les points M tels que M = M’.
b. Déterminer l’affixe du point B’ associé au point B d’affixe 1.
c. Déterminer l’affixe du point C tel que l’affixe de son image C’ soit 2.
2. Étant donné un nombre complexe z, distinct de $i$, on pose $z=x+iy $ et $z’=x’+iy’$ le nombre complexe associé, avec $x,x’,y,y’ $ réels.
a. Déterminer $x’$ et $y’$ en fonction de $x$ et $y$.
b. Déterminer l’ensemble $\Gamma$ des points M, distincts de A, pour lesquels z’ est réel.
c. Placer A, B,B’,C,C’ et représenter $\Gamma$ sur une figure (unité graphique 4 cm).
3. Soit z un nombre complexe différent de $i$.
a. Montrer que l’on a $z’ – i = \dfrac{-1}{z – i}$.
b. On suppose que M, d’affixe z, appartient au cercle $\gamma$ de centre A et de rayon 1. Montrer que M’ appartient à $\gamma$.

🔻Correction Exercice 27

1. a. On a
$\begin{array}{ll} M = M’ &\Leftrightarrow z = \dfrac{i z}{z – i} \\\\ & \Leftrightarrow z^2 – i z = i z \qquad z \ne i \\\\ & \Leftrightarrow z^2 – 2i z = 0 \qquad z \ne i \\\\ & \Leftrightarrow z(z – 2i) = 0 \qquad z \ne i \\\\ & \Leftrightarrow z= 0 ou z = 2i \end{array}$
Les seuls points vérifiant M’ = M sont les points d’affixe 0 et $2i$.
b. Si $z = 1$ alors
$\begin{array}{ll}z’ &= \dfrac{i}{1 – i} \\&= \dfrac{i (1 + i)}{(1 – i)(1 + i)} \\&= \dfrac{-1 + i}{1^2 + 1^2} \\&=\dfrac{-1 + i}{2}\end{array}$.
Le point B’ a donc pour affixe $\dfrac{-1 + i}{2}$
c. On cherche les complexes z tels que :
$\begin{array}{ll} \dfrac{i z}{z- i} = 2 &\Leftrightarrow 2 z -2i = i z \qquad z \ne i \\\\ & \Leftrightarrow z(2 – i) = 2i \qquad z \ne i \\\\ & \Leftrightarrow z = \dfrac{2i}{2 – i} \qquad z \ne i \\\\ & \Leftrightarrow z = \dfrac{2i(2 + i)}{2^2 + 1^2} \\\\ & \Leftrightarrow z= \dfrac{-2 + 4i}{5} \end{array}$
Le point C a pour affixe $\dfrac{-2 + 4i}{5}$
2. a. On a
$\begin{array}{ll} z’ = \dfrac{i(x + i y}{x + i y – i} \\\\ & = \dfrac{-y + i x}{x + i (y – 1)} \\\\ & = \dfrac{-y + i x}{x + i (y – 1)} \times \dfrac{x – i (y – 1)}{x – i (y – 1)} \\\\ & = \dfrac{-xy + i y (y – 1) + i x^2 + x(y – 1)}{x^2 + (y – 1)^2} \\\\ &= \dfrac{-xy + xy – x + i (y^2 – y + x^2)}{x^2 + (y – 1)^2} \\\\ &= \dfrac{-x + i(y^2 – y + x^2)}{x^2 + (y – 1)^2} \end{array}$
Par conséquent $x’ = \dfrac{-x}{x^2 + (y – 1)^2}$ et $y’ = \dfrac{y^2 – y + x^2}{x^2 + (y – 1)^2}$
b. On a
$\begin{array}{ll} z’ réel &\Leftrightarrow y’ = 0 \\\\ & \Leftrightarrow y^2 – y + x^2 = 0 \qquad (x;y) \ne (0;1) \\\\ &\Leftrightarrow x^2 + \left(y – \dfrac{1}{2}\right)^2 – \dfrac{1}{4} = 0 \qquad (x;y) \ne (0;1) \\\\ & \Leftrightarrow x^2 + \left(y – \dfrac{1}{2}\right)^2 = \dfrac{1}{4} \qquad (x;y) \ne (0;1) \end{array}$
Il s’agit du cercle de centre D d’affixe $\dfrac{1}{2}i$ et de rayon $\dfrac{1}{2}$ privé de A.
c.

3) a.
$\begin{array}{ll} z’ – i &= \dfrac{i z}{z – i} – i \\&= \dfrac{ic z – i z – 1}{z – i} \\&= \dfrac{-1}{z i} \end{array}$
b. Si M appartient à $\gamma$ alors $AM = 1$ soit $|z – i| = 1$.
Or :
$\begin{array}{ll} |z’ – i| & = \left|\dfrac{-1}{z – i}\right| \\\\ & = \dfrac{1}{|z – i|} \\\\ &= \dfrac{1}{1} \\\\ & = 1 \end{array}$
Par conséquent M’ appartient également au cercle $\gamma$.