Exercices corrigés - Fonction logarithme Série 2
Exercice 1:
Simplifier l’écriture des expressions suivantes
1) $ \ln (3e) $
2) $ \ln e^2 $
3) $ \ln \left(\sqrt{e}\right) $
4) $ \ln \dfrac{1}{3} + \ln \dfrac{3}{5} + \ln \dfrac{5}{7} + \ln \dfrac{7}{9} $
5) $ \ln \left( 2 +\sqrt{3}\right)^{20} + \ln \left(2-\sqrt{3}\right)^{20}$
1) $ \ln (3e) = \ln 3 + \ln e = \ln 3 + 1 $
2) $ \ln e^2 = 2\ln e = 2$
3) $ \ln \left(\sqrt{e}\right) = \dfrac{1}{2} \ln e = \dfrac{1}{2}$
4) $ \ln \dfrac{1}{3} + \ln \dfrac{3}{5} + \ln \dfrac{5}{7} + \ln \dfrac{7}{9} $ =$\ln 1-\ln 3 + \ln 3-\ln 5 + \ln 5-\ln 7 + \ln 7-\ln 9 $= $-\ln 9$
5)
$ \begin{array}{ll}
\ln \left( 2 +\sqrt{3}\right)^{20} + \ln \left(2-\sqrt{3}\right)^{20} &= \ln \left( \left( 2 +\sqrt{3}\right)^{20} \times \left( 2 -\sqrt{3}\right)^{20} \right) \\\\
&= \ln \left(\left( 2 +\sqrt{3}\right)\left(2-\sqrt{3}\right)\right)^{20} \\\\
&= 20 \ln\left(\left( 2 +\sqrt{3}\right)\left(2-\sqrt{3}\right)\right) \\\\
&= 20 \ln (4-3) \\\\
&= 20 \ln 1 \\\\
&= 0
\end{array}$
Exercice 2:
Résoudre les équations proposées après avoir fourni l’ensemble d’étude.
1) $ \ln 3x = 8$
2) $ \ln x = -2$
3) $ \ln x^2 = 1$
4) $ \ln \dfrac{x}{3} = 2$
5) $ \ln x^3 = -3$
6) $ \ln (3x-2) = 0$
7) $ \ln(x^2-1) = \ln 4 + \ln 2$
8) $ \ln (x^2-3x + 2) = \ln 9$.
9) $ \ln (2x + 1) + \ln (-x + 1) = 0$
10) $ \ln (x-1)^2-\ln (x+ 1) = 0$
11) $ e^{3x + 4} = 2$
12) $ e^{-x \ln 4} = 5$
13) $ e^x + e^{-x}-6 = 0$
Dans chacun des cas on vérifie que les solutions appartiennent bien à l’intervalle d’étude.
1) L’ensemble d’étude est tel que $ 3x > 0$ soit $ ]0;+ \infty[$.
$ \begin{array}{ll} \ln 3x = 8 &\Leftrightarrow \ln 3x = \ln e^8 \\&\Leftrightarrow 3x = e^8 \\&\Leftrightarrow x = \dfrac{e^8}{3} \end{array}$
La solution de l’équation est $ \dfrac{e^8}{3}$.
2) L’ensemble d’étude est tel que $ x > 0 $soit $ ]0;+\infty[$.
$ \ln x = -2 \Leftrightarrow \ln x = \ln e^{-2} \Leftrightarrow x = e^{-2}$
La solution de l’équation est $ e^{-2}$.
3) L’ensemble d’étude est tel que $ x^2 > 0$ soit $]-\infty;0[\cup ]0;+\infty[$.
$ \begin{array}{ll} \ln x^2 = 1 &\Leftrightarrow \ln x^2 = \ln e \\&\Leftrightarrow x^2 = e \\&\Leftrightarrow x = \sqrt{e} ou x = -\sqrt{e}\end{array}$.
Les solutions de l’équation sont $-\sqrt{e} et \sqrt{e}$.
4) L’ensemble d’étude est tel que $ \dfrac{x}{3} > 0$ soit $ ]0;+\infty[$.
$ \begin{array}{ll} \ln \dfrac{x}{3} = 2 &\Leftrightarrow \ln \dfrac{x}{3} = \ln e^2 \\&\Leftrightarrow \dfrac{x}{3} = e^2 \\&\Leftrightarrow x = 3 e^2\end{array}$.
La solution de l’équation est $ 3 e^2$.
5) L’ensemble d’étude est tel que $ x^3 > 0 $soit $ ]0;+\infty[$.
$ \begin{array}{ll} \ln x^3 = -3 &\Leftrightarrow \ln x^3 = \ln e^{-3} \\&\Leftrightarrow x^3 = e^{-3} \\&\Leftrightarrow x = \sqrt[3]{e^{-3}} \\&\Leftrightarrow x = e^{-1}\end{array}$.
La solution de l’équation est $ e^{-1}$.
6) L’ensemble d’étude est tel que $ 3x-2 > 0$ soit $ ]\dfrac{2}{3};+\infty[$.
$\begin{array}{ll} \ln (3x-2) = 0 &\Leftrightarrow \ln (3x-2) = \ln 1 \\&\Leftrightarrow 3x-2 = 1 \\&\Leftrightarrow 3x = 3 \\&\Leftrightarrow x = 1 \end{array} $ .
La solution de l’équation est 1.
7) L’ensemble d’étude est tel que $ x^2-1 > 0$ soit $ ]-\infty;-1[\cup]1;+\infty[$.
$\begin{array}{ll} \ln(x^2-1) = \ln 4 + \ln 2 &\Leftrightarrow \ln (x^2-1) = \ln (4 \times 2) \\\\
&\Leftrightarrow x^2-1 = 8 \\\\
&\Leftrightarrow x^2 = 9 \\\\
&\Leftrightarrow x = -3 ou x = 3\end{array} $
Les solutions sont -3 et 3.
8) L’ensemble d’étude est tel que $ x^2-3x + 2 > 0$
$ \Delta = (-3)^2-4 \times 2 = 1$.
Les racines sont donc $ x_1 = \dfrac{3-1}{2} = 1$ et$ x_2 = \dfrac{3 + 1}{2} = 2$.
Par conséquent l’ensemble d’étude est $ ]-\infty;1[\cup]2;+\infty[$.
$ \begin{array}{ll} \ln (x^2-3x + 2) = \ln 9& \Leftrightarrow x^2-3x + 2 = 9 \\&\Leftrightarrow x^2-3x-7 = 0\end{array} $
$ \Delta = (-3)-4 \times (-7) = 37$
Il y a deux racines : $ \dfrac{3-\sqrt{37}}{2}$ et $ \dfrac{3 + \sqrt{37}}{2}$.
Ces deux racines appartiennent bien à l’ensemble d’étude.
Les solutions de l’équation sont donc $ \dfrac{3-\sqrt{37}}{2}$ et $ \dfrac{3 + \sqrt{37}}{2}$.
9) L’ensemble d’étude est tel que $ 2x +1 > 0$ et $ -x + 1 > 0$.
$ 2x + 1 > 0 \Leftrightarrow x >-\dfrac{1}{2}$
$ -x + 1 > 0 \Leftrightarrow x < 1$.
L’ensemble d’étude est donc $ ]-\dfrac{1}{2};1[$.
$ \begin{array}{ll} \ln (2x + 1) + \ln (-x + 1) = 0 &\Leftrightarrow \ln \left((2x + 1)(-x + 1)\right) = \ln 1 \\\\
&\Leftrightarrow (2x + 1)(-x + 1) = 1 \\\\
&\Leftrightarrow -2x^2 + 2x-x +1 = 1 \\\\
&\Leftrightarrow -2x^2 +x = 0 \\\\
&\Leftrightarrow x(-2x + 1) = 0 \\\\
&\Leftrightarrow x = 0\ ou\ x = \dfrac{1}{2}\end{array} $
Les solutions sont $ 0 $ et $ \dfrac{1}{2}$.
10) L’ensemble d’étude est tel que $ (x-1) ^2 > 0$ et $ x + 1 > 0$.
$ (x – 1)^2 > 0 \Leftrightarrow x \ne 1$
$ x + 1 > 0 \Leftrightarrow x >-1$
L’ensemble d’étude est donc $ ]-1; 1[ \cup ]1;+\infty[$.
$ \begin{array}{ll} \ln (x-1)^2-\ln (x+ 1) = 0 &\Leftrightarrow \ln\dfrac{(x-1)^2}{x + 1} = \ln 1 \\\\
&\Leftrightarrow \dfrac{(x-1)^2}{x + 1} = 1 \\\\
&\Leftrightarrow \dfrac{(x-1)^2}{x + 1}-1 = 0 \\\\
&\Leftrightarrow \dfrac{(x-1)^2}{x + 1}-\dfrac{x + 1}{x + 1} = 0 \\\\
&\Leftrightarrow \dfrac{x^2-2x + 1-x-1}{x + 1} = 0 \\\\
&\Leftrightarrow \dfrac{x^2-3x}{x + 1} = 0 \\\\
&\Leftrightarrow \dfrac{x(x-3)}{x + 1} = 0\end{array} $
Les solutions de l’équation sont donc 0 et 3.
11) L’intervalle d’étude est $ \mathbb{R} $.
$ \begin{array}{ll} e^{3x + 4} = 2 &\Leftrightarrow e^{3x + 4} = e^{\ln 2} \\\\
& \Leftrightarrow 3x + 4 = \ln 2 \\\\
&\Leftrightarrow 3x = \ln 2-4 \\\\
& \Leftrightarrow x = \dfrac{\ln 2-4}{3}\end{array} $
La solution de l’équation est $ \dfrac{\ln 2-4}{3}$
12) L’intervalle d’étude est $ \mathbb{R} $.
$ \begin{array}{ll} e^{-x \ln 4} = 5& \Leftrightarrow e^{-x \ln 4} = e^{\ln 5} \\&\Leftrightarrow -x \ln 4 = \ln 5 \\&\Leftrightarrow x =-\dfrac{\ln 5}{\ln 4}\end{array} $
La solution est $-\dfrac{\ln 5}{\ln 4}$
13) L’intervalle d’étude est$\mathbb{R}$.
$\begin{array}{ll} e^x + e^{-x}-6 = 0 &\Leftrightarrow e^{-x}\left(\left(e^x \right)^2 + 1-6 e^x\right) = 0 \\&\Leftrightarrow \left(e^x \right)^2 + 1-6 e^x = 0\end{array} $
Posons$ X = e^x$
On obtient ainsi $X^2 + 1 -6X = 0$.
$\Delta = (-6)^2-4 = 32$
Les solutions sont $X_1 = \dfrac{6-\sqrt{32}}{2} $ et $X_2 = \dfrac{6 + \sqrt{32}}{2}$.
Ces deux racines sont strictement positives.
$e^x = X_1 \Leftrightarrow x = \ln \dfrac{6 -\sqrt{32}}{2}$
$e^x = X_2 \Leftrightarrow x = \ln \dfrac{6 + \sqrt{32}}{2}$.
Les solutions de l’équation sont $ \ln \dfrac{6 + \sqrt{32}}{2} $ et $\ln \dfrac{6 – \sqrt{32}}{2}$.
Exercice 3:
Résoudre les inéquations proposées après avoir fourni l’ensemble d’étude.
1) $1-2\ln 2x \ge 0 $
2) $3-\ln x \le 0$
3) $2 + 3\ln 2x \le 0$
4) $\ln (5-x)-\ln 3 + \ln (x-1) \ge 0$
5) $ \ln(3x^2-x-2) \ge \ln(6x + 4) $
1) L’ensemble d’étude est tel que $2x > 0 $soit $]0;+\infty[$
$\begin{array}{ll} 1-2\ln 2x \ge 0 &\Leftrightarrow -2 \ln 2x \ge -1 \\\\
&\Leftrightarrow \ln 2x \le \dfrac{1}{2} \\\\
&\Leftrightarrow \ln 2x \le \ln e^{1/2} \\\\
& \Leftrightarrow 2x \le e^{1/2} \\\\
&\Leftrightarrow x \le \dfrac{e^{1/2}}{2}\end{array} $
La solution de l’inéquation est $]0;\dfrac{e^{1/2}}{2}] $.
2) L’ensemble d’étude est tel que $x > 0 $soit $]0;+\infty[$.
$\begin{array}{ll} 3-\ln x \le 0 &\Leftrightarrow-\ln x \le -3\\& \Leftrightarrow \ln x \ge 3 \\&\Leftrightarrow \ln x \ge \ln e^3 \\&\Leftrightarrow x \ge e^3\end{array} $
La solution de l’inéquation est $[ e^3;+\infty [$.
3) L’ensemble d’étude est tel que $2x > 0 $soit $]0;+\infty[$.
$\begin{array}{ll} 2 + 3\ln 2x \le 0 &\Leftrightarrow 3\ln 2x \le -2 \\\\
& \Leftrightarrow \ln 2x \le-\dfrac{2}{3} \\\\
& \Leftrightarrow \ln 2x \le \ln e^{-2/3} \\\\
&\Leftrightarrow 2x \le e^{-2/3} \\\\
& \Leftrightarrow x \le \dfrac{e^{-2/3}}{2} \end{array}$
La solution de l’inéquation est $] 0;\dfrac{e^{-2/3}}{2} ] $
4) L’ensemble d’étude est tel que $5-x > 0 et x-1 > 0$
$5-x > 0 \Leftrightarrow x < 5$
$ x-1 > 0 \Leftrightarrow x > 1$
L’ensemble d’étude est donc $]1;5[$.
$ \begin{array}{ll} \ln (5-x)-\ln 3 + \ln (x-1) \ge 0 &\Leftrightarrow \ln \dfrac{(5-x)(x-1)}{3} \ge \ln 1 \\\\
&\Leftrightarrow \dfrac{(5-x)(x-1)}{3} \ge 1 \\\\
&\Leftrightarrow \dfrac{(5-x)(x-1)}{3}-\dfrac{3}{3} \ge 0 \\\\
&\Leftrightarrow \dfrac{5x-5-x^2 + x-3}{3} \ge 0 \\\\
&\Leftrightarrow \dfrac{-x^2 + 6x-8}{3} \ge 0 \end{array} $
$\Delta = 6^2-4 \times 8 = 4$.
Les racines sont $\dfrac{-6-2}{-2} = 4$ et $\dfrac{-6 + 2}{-2} = 2$.
La solution de l’inéquation est donc $[2;4] $.
5) L’ensemble d’étude est tel que $3x^2-x-2 > 0 $ et $6x + 4 > 0$
$3x ^2-x – 2 > 0 $
$\Delta = (-1)^2-4 \times 3 \times (-2) = 25$.
Les racines sont $\dfrac{1-5}{6} = \dfrac{-2}{3}$ et $\dfrac{1 + 5}{6} = 1$.
$3x ^2-x – 2 > 0 \Leftrightarrow ]-\infty;\dfrac{-2}{3}[ \cup ]1;+\infty[$.
$6x + 4 > 0 \Leftrightarrow x > \dfrac{-2}{3}$.
L’intervalle d’étude est donc $]1;+\infty[$
$\begin{array}{ll} \ln(3x^2-x-2) \ge \ln(6x + 4) &\Leftrightarrow 3x^2-x-2 \ge 6x + 4 \\&\Leftrightarrow 3x^2-7x-6 \ge 0\end{array}$
$\Delta = (-7)^2-4 \times 3 \times (-6) = 121$
Les racines sont $\dfrac{7-11}{6} = \dfrac{-2}{3} < 1$ et $\dfrac{7 + 11}{6} = 3$.
La solution de l’inéquation est $[3;+\infty[$.
Exercice 4:
Dans chacun des cas, déterminer l’ensemble sur lequel la fonction$f$est dérivable puis calculer leur dérivée et enfin déterminer leur sens de variation.
1) $f(x) = x\ln x$
2) $ f(x) = \sqrt{\ln x}$
3) $f(x) = \dfrac{1}{\ln x}$
4) $f(x) = \left(\dfrac{x}{\ln x}\right)^2$
5) $f(x) = \left(\ln x \right)^3 $
1) La fonction $f $est dérivable sur $]0;+\infty[$.
$f'(x) = \ln x + \dfrac{x}{x} = \ln x + 1$
$\begin{array}{ll} f'(x) > 0 &\Leftrightarrow \ln x +1 > 0 \\&\Leftrightarrow \ln x >-1 \\&\Leftrightarrow x > e^{-1}\end{array}$.
La fonction $f $est donc décroissante sur $]0;e^{-1}] $ et croissante sur $[e^{-1};+\infty[$ .
2) Pour que la fonction$f$soit dérivable, il faut que $x > 0$ et $\ln x > 0$.
La fonction$f$est donc dérivable sur $]1;+\infty[$.
$f'(x) = \dfrac{\dfrac{1}{x}}{2\ln x} > 0 $sur $]1;+\infty[$.
La fonction$f$est donc croissante sur $ [1;+\infty[$.
3) La fonction$f$est dérivable sur$ ]0;1[\cup]1;+\infty[$.
$f'(x) =-\dfrac{\dfrac{1}{x}}{\left(\ln x\right)^2} < 0$ sur $]0;1[\cup]1;+\infty[$.
La fonction$f$est décroissante sur $]0;1[\cup]1;+\infty[$
4) La fonction $f$est dérivable sur$ ]0;1[\cup]1;+\infty[$.
$f'(x) = 2 \dfrac{\ln x-\dfrac{x}{x}}{\left(\ln x\right)^2} \times \dfrac{x}{\ln x} = 2\dfrac{\ln x-1}{\left(\ln x\right)^2} \times \dfrac{x}{\ln x}$
$f'(x) $est du signe de $\dfrac{\ln x-1}{\ln x}$.
$\ln x-1 > 0 \Leftrightarrow x > e$
$\ln x > 0 \Leftrightarrow x > 1$
Par conséquent $f'(x) > 0$ sur $]0;1[ \cup ]e;+\infty[$ et $f'(x) <0 $sur $]1;e[$
La fonction $f $est donc décroissante sur $]1;e[$ et croissante sur $]0;1[ \cup ]e;+\infty[ $.
5) $ f $ est dérivable sur $]0;+\infty[$.
$f'(x) = \dfrac{3}{x} \times \left(\ln x \right)^2 > 0$ sur $]0;+\infty[$ .
La fonction $f $est donc croissante sur $]0;+\infty[$.
Exercice 5:
On considère la fonction$f$définie sur $]0;+\infty[ $ par $f(x) = e^x-\ln x$
1) Étudier les variations de la fonction $\varphi $définie sur$\mathbb{R}$ par :
$\varphi(x) = xe^x-1$
2) En déduire qu’il existe un réel unique $ \alpha$ tel que $\alpha e^{\alpha}= 1$.
Donner un encadrement d’amplitude $10^{-3}$ de $\alpha$.
3) Étudier le signe de $ \varphi(x) $.
4) Calculer la fonction dérivée $f’ $ de$f$et étudier son signe sur $]0;+\infty[$.
5) En déduire les variations de la fonction $f$.
6) Montrer que$f$admet un minimum $m $ égal à $\alpha + \alpha^{-1}$.
1) La fonction $\varphi $ est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables sur $\mathbb{R}$.
$\varphi'(x) = e^x + xe^x = (1 + x)e^x$.
$\varphi'(x) $ est donc du signe de $1 + x$.
La fonction $\varphi$ est donc décroissante sur $]-\infty;-1] $ et croissante sur $ [-1;+\infty$.
2) $\lim\limits_{x \to -\infty} xe^x = 0 $donc$ \lim\limits_{x \to -\infty} \varphi(x) = -1$
$\lim\limits_{x \to +\infty} e^x = +\infty $donc $\lim\limits_{x \to +\infty} \varphi(x) = +\infty$.
$ \varphi(-1) = -e^{-1}-1$.
Par conséquent :
– sur l’intervalle $]-\infty;-1], \varphi(x) < -1$. L’équation $\varphi(x) = 0$ ne possède pas de solution sur cet intervalle.
– sur l’intervalle$ [-1;+\infty[$, la fonction$ \varphi $est continue (car dérivable) et strictement croissante.
$0$ appartient à l’intervalle image.
D’après le théorème des valeurs intermédiaires, l’équation $\varphi(x) = 0$ admet une unique solution sur cette intervalle.
Par conséquent, il existe un unique réel $\alpha$ tel que $\alpha e^{\alpha} = 1$.
D’après la calculatrice $0,692 < \alpha < 0,693$.
3) Cela signifie donc que :
$\varphi $est strictement négative sur $]-\infty;\alpha[$
$ \varphi(\alpha) = 0$
$\varphi$ est strictement positive sur $]\alpha;+\infty[$.
4) La fonction$f$est dérivable sur $]0;+\infty[$.
$f'(x) = e^x-\dfrac{1}{x} = \dfrac{xe^x-1}{x} = \dfrac{\varphi(x)}{x}$
Sur $]0;+\infty[$, le signe de $f'(x) $ ne dépend que de celui de$ \varphi(x) $.
Par conséquent $f'(x) \le 0$ sur $]0;\alpha] $et $f'(x) \ge 0$ sur $ [\alpha;+\infty[$.
5) La fonction$f$est donc décroissante sur $]0;+\alpha] $ et croissante sur $ [\alpha;+\infty[$.
6) Elle admet donc un minimum en $\alpha$.
$ f(\alpha) = e^{\alpha}-\ln \alpha$.
Mais $\alpha e^{\alpha} = 1 $soit $e^{\alpha} = \dfrac{1}{\alpha}$ et $\alpha = e^{-\alpha}$.
Par conséquent $f(\alpha) = \dfrac{1}{\alpha}-\ln e^{-\alpha} = \dfrac{1}{\alpha} + \alpha$.
Exercice 6:
Propriétés algébriques – Pour s’entraîner
Exprimer chacun des nombres suivants en fonction de $\ln 3$.
1) $\ln \left( \dfrac{1}{9} \right) $
2) $\ln 24-\ln 216$
3) $\ln \dfrac{3}{4} + \ln 4$
4) $2\ln 3-\ln 27$
5) $\ln \left( 9\sqrt{3} \right) $
1) $\ln \left( \dfrac{1}{9} \right)=-\ln 9$$=-\ln\left(3^2\right)=-2\ln 3$
2) $ \ln 24-\ln 216=\ln\left(\dfrac{24}{216}\right) $$=\ln \left(\dfrac{1}{9}\right)=-2\ln 3$
3) $\ln \dfrac{3}{4} + \ln 4=\ln \left(\dfrac{3}{4}\times 4\right)=\ln 3$
4) $2\ln 3-\ln 27=2\ln 3\ln \left(3^3\right) $$=2\ln 3-3\ln 3=-\ln 3$
5) $\ln \left( 9\sqrt{3} \right)=\ln 9 + \ln \sqrt{3}$$=2\ln 3+\dfrac{1}{2}\ln 3=\dfrac{5}{2}\ln 3$
Exercice 7:
Propriétés algébriques – Pour s’entraîner
Exprimer chacun des nombres suivants en fonction de $lnx$.
1) $ \ln \left( \dfrac{x}{3} \right) $
2) $ \ln \sqrt{x}$
3) $ \ln \dfrac{x}{4} + \ln x $
4) $2\ln x-\ln \left( x^{45} \right) $
5) $ \ln \left( 9\sqrt{x} \right) $
1) $\ln \left( \dfrac{x}{3} \right)=\ln x-\ln 3 $
2) $\ln \sqrt{x}=\dfrac{1}{2}\ln x $
3) $\ln \dfrac{x}{4} + \ln x=\ln x-\ln 4+\ln x=2\ln x+\ln 4 $
4) $2\ln x-\ln \left( x^{45} \right)=2\ln x-45\ln x=-43\ln x $
5) $\ln \left( 9\sqrt{x} \right)=\ln 9+\ln \sqrt{x}=2\ln 3+\dfrac{1}{2}\ln x $
Exercice 8:
Équations et inéquations – Pour s’entraîner
Résoudre :
1) $ \ln (2-3x) \ge 0 $
2) $ \ln(2-x)+1=0 $
3) $ \ln(x+5)=\ln3 $
4) $ \ln \left( \dfrac{3}{x} \right) \ge \ln 3 $
5) $ e^x \le \dfrac{1}{2} $
6) $ \ln \left( \dfrac{3x-1}{x+2} \right) \ge 0 $
7) $ 2 \left( \ln(x-1) \right) ^{2} +5 \ln(x-1)-15 = 0 $
1) $\ln (2-3x) \ge 0$
On cherche dans un premier temps l’intervalle d’étude.
Il faut que $2-3x>0 \Leftrightarrow x<\dfrac{2}{3}$.
Sur $]-\infty;\dfrac{2}{3}[ $ on a :
$\begin{array}{ll} \ln(2-3x) \ge 0 &\Leftrightarrow \ln(2-3x) \ge \ln 1 \\
&\Leftrightarrow 2-3x \ge 1 \\
&\Leftrightarrow -3x \ge -1 \\
&\Leftrightarrow x\le \dfrac{1}{3}
\end{array}$
La solution de l’inéquation est donc $]-\infty;\dfrac{1}{3}]$.
2) $ \ln(2-x)+1=0$
On cherche dans un premier temps l’intervalle d’étude.
Il faut que $2-x>0 \Leftrightarrow x<2 $ .
Sur $ ]-\infty;2[$ on a :
$\begin{array}{ll}
\ln(2-x)+1=0 &\Leftrightarrow \ln(2-x)=-1 \\
&\Leftrightarrow \ln(2-x)=\ln \left(e^{-1}\right) \\
&\Leftrightarrow 2-x=e^{-1} \\
&\Leftrightarrow -x=e^{-1}-2 \\
&\Leftrightarrow x=2-e^{-1}
\end{array}$
La solution de l’équation est $2-e^{-1} $.
3) $ \ln(x+5)=\ln3 $
On cherche dans un premier temps l’intervalle d’étude.
Il faut que $x+5>0 \Leftrightarrow x>-5$.
Sur $]-5;+\infty[$ on a :
$\begin{array}{ll} \ln(x+5)=\ln 3 &\Leftrightarrow x+5=3 \\
&\Leftrightarrow x=-2
\end{array} $
La solution de l’équation est $-2$.
4) $ \ln \left( \dfrac{3}{x} \right) \ge \ln 3$
On cherche dans un premier temps l’intervalle d’étude.
Il faut que$ \dfrac{3}{x}>0 \Leftrightarrow x>0$.
Sur $]0;+\infty[ $ on a :
$\begin{array}{ll} \ln\left( \dfrac{3}{x}\right)\ge\ln 3 &\Leftrightarrow \dfrac{3}{x} \ge3\\
&\Leftrightarrow 0< \dfrac{x}{3}\le\dfrac{1}{3}\\
&\Leftrightarrow 0< x\le1\end{array}$
La solution de l’inéquation est $]0;1] $.
5) $ e^x \le \dfrac{1}{2} \Leftrightarrow x \le \ln \dfrac{1}{2} \Leftrightarrow x \le -\ln 2$
La solution de l’inéquation est $]-\infty;-\ln 2] $.
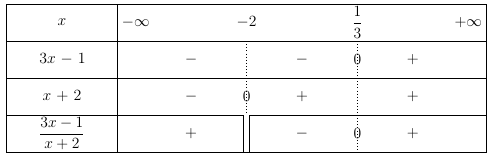
6) $ \ln \left( \dfrac{3x-1}{x+2} \right) \ge 0$
On cherche dans un premier temps l’intervalle d’étude .
Il faut que $\dfrac{3x-1}{x+2} >0$.
$ 3x-1=0 \Leftrightarrow x=\dfrac{1}{3} et 3x-1>0 \Leftrightarrow x > \dfrac{1}{3}$
$ x+2=0 \Leftrightarrow x=-2 et x+2>0 \Leftrightarrow x>-2$
Sur $]-\infty;-2[\cup]\dfrac{1}{3};+\infty[$ on a :
$\begin{array}{ll} \ln \left( \dfrac{3x-1}{x+2} \right) \ge 0 &\Leftrightarrow \ln \left( \dfrac{3x-1}{x+2} \right) \ge \ln 1 \\
&\Leftrightarrow \dfrac{3x-1}{x+2} \ge 1 \\
&\Leftrightarrow \dfrac{3x-1}{x+2}-1 \ge 0 \\
&\Leftrightarrow \dfrac{3x-1-x-2}{x+2} \ge 0 \\
&\Leftrightarrow \dfrac{2x-3}{x+2} \ge 0
\end{array}$
$ 2x-3=0 \Leftrightarrow x=\dfrac{3}{2} et 2x-3>0 \Leftrightarrow x > \dfrac{3}{2}$
$ x+2=0 \Leftrightarrow x=-2 et x+2>0 \Leftrightarrow x>-2$
Ainsi la solution de l’inéquation est $]-\infty;-2[\cup[\dfrac{3}{2};+\infty[$.
7) $ 2 \left( \ln(x-1) \right) ^{2} +5 \ln(x-1)-15 = 0$
On résout cette équation sur $]1;+\infty[$.
On pose $X=\ln(x-1) $
On obtient ainsi l’équation$ 2X^2+5X-15=0$
Le discriminant est $\Delta=5^2-4\times 2\times (-15)=145>0$
Les solutions sont donc $\dfrac{-5-\sqrt{145}}{4}$ et $\dfrac{-5+\sqrt{145}}{4}$.
On résout maintenant sur $]1;+\infty[$ les équations : $\ln(x-1)=\dfrac{-5-\sqrt{145}}{4}$
$\begin{array}{ll|l}
\ln(x-1)=\dfrac{-5+\sqrt{145}}{4} &\Leftrightarrow x-1=\exp\left(\dfrac{-5-\sqrt{145}}{4}\right) \\&\Leftrightarrow x-1=\exp \left(\dfrac{-5+\sqrt{145}}{4}\right) \\
&\Leftrightarrow x=1+\exp\left(\dfrac{-5-\sqrt{145}}{4}\right)\\&\Leftrightarrow x=1+\exp\left(\dfrac{-5+\sqrt{145}}{4}\right)
\end{array}$
Les solutions de l’équation sont $1+\exp\left(\dfrac{-5-\sqrt{145}}{4}\right) $ et $1+\exp\left(\dfrac{-5+\sqrt{145}}{4}\right) $
Exercice 9:
Limites – Pour s’entraîner
Déterminer les limites suivantes
1) $\lim\limits_{x \to +\infty} \left( \ln x \right) ^{2}-\ln x$
2) $\lim\limits_{x \to +\infty} \ln x-2x $
3) $\lim\limits_{x \to 0^+} \left( \ln x \right) ^{2}-3\ln x $
4) $\lim\limits_{x \to +\infty} \ln \left( x^2 +105x + 18\right) $
1) $\lim\limits_{x \to +\infty}\ln x=+\infty $
$\lim\limits_{X \to +\infty} X^2-X=\lim\limits_{X \to +\infty} X^2=+\infty$ d’après la limite des termes de plus haut degré.
Donc $\lim\limits_{x \to +\infty} \left( \ln x \right) ^{2}-\ln x=+\infty$
2) $\ln x-2x=x\left(\dfrac{\ln x}{x}-2\right) $
Or $\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0$
Donc $\lim\limits_{x \to +\infty} \ln x-2x=-\infty$
3) $\lim\limits_{x \to 0^+} \ln x=-\infty$
Donc $ \lim\limits_{x \to 0^+} \left(\ln x\right)^2=+\infty$ et $\lim\limits_{x \to 0^+} -3\ln x=+\infty$.
Par consequent $ \lim\limits_{x \to 0^+} \left( \ln x \right) ^{2}-3\ln x =+\infty$
4) $\lim\limits_{x \to +\infty} \ln \left( x^2 +105x + 18\right) $
$\lim\limits_{x \to +\infty} x^2+105x-18=\lim\limits_{x \to +\infty} x^2=+\infty$ d’après la limite des termes de plus haut degré.
$\lim\limits_{X \to +\infty} \ln X=+\infty $
Donc $\lim\limits_{x \to +\infty} \ln\left(x^2+105x+18\right)=+\infty $.
Exercice 10:
Limites – Pour s’entraîner
1) $Démontrer que \lim\limits_{x \to 0} \dfrac{\ln(1+x)}{x}=1$
2) $Calculer \lim\limits_{x \to +\infty} x\ln \left( 1 + \dfrac{1}{x} \right) $
3) $Calculer \lim\limits_{x \to +\infty} e^x \ln \left( 1+e^{-x} \right) $
4) $Calculer \lim\limits_{x \to 0} \dfrac{\ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}$
1) $t(x)=\dfrac{\ln(1+x)}{x}=\dfrac{\ln(1+x)-\ln 1}{1+x-1}$
Donc $ \lim\limits_{x \to 0} \dfrac{\ln(1+x)}{x}=f'(0) $ (limite du taux d’accroissement $ t(x)) $ où $f(x)=\ln(1+x) $
Or $f'(x)=\dfrac{1}{x+1}$ donc $f'(0)=1 $
Ainsi $ \lim\limits_{x \to 0} \dfrac{\ln(1+x)}{x}=1$
2) Si on pose$ X=\dfrac{1}{x}$ alors $ x\ln \left( 1 + \dfrac{1}{x} \right)=\dfrac{\ln(1+X)}{X}$
Donc $\lim\limits_{x \to +\infty} x\ln \left( 1 + \dfrac{1}{x} \right)= \lim\limits_{X \to 0^+} \dfrac{\ln(1+x)}{x}=1$
3) Si on pose $X=e^{-x}$ alors $ e^x \ln \left( 1+e^{-x} \right)=\dfrac{\ln(1+X)}{X}$
Donc$ \lim\limits_{x \to +\infty} e^x \ln \left( 1+e^{-x} \right) =\lim\limits_{X \to 0^+} \dfrac{\ln(1+x)}{x}=1$
Si on pose $X=\sqrt{X}$ alors $\dfrac{\ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}=\dfrac{\ln(1+X)}{X}$
Donc $ \lim\limits_{x \to 0} \dfrac{\ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}=\lim\limits_{X \to 0^+} \dfrac{\ln(1+x)}{x}=1$
Exercice 11:
Déterminer l’ensemble de définition et les limites aux bornes des fonctions définies par :
1) $f_1(x)=\dfrac{1}{\ln(x)} $
2) $f_2(x)=\ln\left(x^2+2x+3\right) $
3) $f_3(x)=x-\ln x $
1) La fonction $ f_1$ est définie sur $I=]0;1[\cup]1;+\infty[ $ (il faut que$ x>0$ et que$ \ln x\neq 0$).
$\bullet \lim\limits_{x\to 0^+} \ln x=-\infty donc \lim\limits_{x \to 0^+} f_1(x)=0^-$
$\bullet \lim\limits_{x\to 1^-} \ln x=0^- donc \lim\limits_{x \to 1^-} f_1(x)=-\infty $
$\bullet \lim\limits_{x\to 1^+} \ln x=0^+ donc \lim\limits_{x \to 1^+} f_1(x)=+\infty $
$\bullet \lim\limits_{x\to +\infty} \ln x=+\infty donc \lim\limits_{x \to 1^-} f_1(x)=0 $
2) On étudie dans un premier temps le signe de $ x^2+2x+3$.
$\Delta=2^2-4\times 3\times 1=-8<0$. Le coefficient principal est $a=1> 0$.
Donc l’expression est toujours strictement positive.
Ainsi la fonction$ f_2 $ est définie sur $\mathbb{R}$.
$\bullet \lim\limits_{x\to -\infty} x^2+2x+3=\lim\limits_{x \to -\infty} x^2=+\infty$ d’après la limite des termes de plus haut degré.
De plus$ \lim\limits_{X \to +\infty} \ln X=+\infty$.
Donc$ \lim\limits_{x \to -\infty} f_2(x)=+\infty $
$\bullet \lim\limits_{x\to +\infty} x^2+2x+3=\lim\limits_{x \to +\infty} x^2=+\infty $d’après la limite des termes de plus haut degré.
De plus$ \lim\limits_{X \to +\infty} \ln X=+\infty$.
Donc $\lim\limits_{x \to +\infty} f_2(x)=+\infty $
3) La fonction $f_3 $ est définie sur $]0;+\infty[ $
$\bullet \lim\limits_{x \to 0^+} x=0 et \lim\limits_{x \to 0^+} \ln x=-\infty$ donc $\lim\limits_{x \to 0^+} f_3(x)=+\infty$
$\bullet f_3(x)=x\left(1-\dfrac{\ln x}{x}\right) $.
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0 $ donc $\lim\limits_{x \to +\infty} f_3(x)=+\infty$.
Exercice 12:
Déterminer l’ensemble de définition des fonctions et les limites indiquées.
1) $f_1(x)= \dfrac{\ln(1+x)}{x^2}$ et $ \lim\limits_{x \to 0^+} f_1(x) $
2) $f_2(x)=x+x\ln\left(1+\dfrac{1}{x}\right) $ et $\lim\limits_{x \to +\infty} f_2(x) $
3) $f_3(x)=\dfrac{\ln x}{x^4}$ et $ \lim\limits_{x \to +\infty} f_3(x) $
1) $\ln(1+x) $ existe pour tout $x\in ]-1;+\infty[$.
Donc $ f_1 $est définie sur $]-1;0[\cup]0;+\infty[$.
$f_1(x)=\dfrac{1}{x}\times \dfrac{\ln(1+x)}{x}$.
Or $ \lim\limits_{x \to 0^+} \dfrac{\ln(1+x)}{x}=1 $ et $\lim\limits_{x \to 0^+} \dfrac{1}{x}=+\infty $
Donc$ \lim\limits_{x \to 0} f_1(x)=+\infty$.
2) Il faut que$ 1+\dfrac{1}{x}>0 \Leftrightarrow \dfrac{1+x}{x}>0$.
Donc$ f_2 $ est définie sur $ ]-\infty;-1[\cup]0;+\infty[$.
$f_2(x)=x\left(1+\ln \left(1+\dfrac{1}{x}\right)\right) $
$\lim\limits_{x \to +\infty} 1+\dfrac{1}{x}=1$ ainsi $\lim\limits_{x \to +\infty} 1+\ln \left(1+\dfrac{1}{x}\right)=1$.
Par conséquent $\lim\limits_{x \to +\infty} f_2(x)=+\infty$.
$f_3 $ est définie sur $]0;+\infty[$.
$f_3(x)=\dfrac{1}{x^3} \times \dfrac{\ln x}{x}$
Or $\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0$ et $\lim\limits_{x \to +\infty} \dfrac{1}{x^3}=0$.
Donc $ \lim\limits_{x \to +\infty} f_3(x)=0$.
Exercice 13:
On considère la fonction$f$définie par $f(x)=\dfrac{\ln x}{x+1}$.
1) Déterminer l’ensemble de définition de la fonction $f$.
2) Déterminer les limites aux bornes.
3) En déduire l’existence d’asymptotes.
4) Déterminer une équation de la tangente à la courbe $ \mathscr{C}$
représentant la fonction$f$au point d’abscisse 1.
1) La fonction$f$est définie sur$ ]0;+\infty[$.
2) $\lim\limits_{x \to 0^+} \ln x=-\infty et \lim\limits_{x \to 0^+} x+1=1$ donc $\lim\limits_{x \to 0^+} f(x)=-\infty $
$f(x)=\dfrac{x}{x+1}\times \dfrac{\ln x}{x}$
D’après la limite des termes de plus haut degré, on a $ \lim\limits_{x \to +\infty} \dfrac{x}{x+1}=\lim\limits_{x \to +\infty} \dfrac{x}{x}=1$
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0$
Donc$ \lim\limits_{x \to +\infty} f(x)=0$.
3) Il y a donc deux asymptotes d’équation $ x=0$ et $y=0$.
4) Une équation de la tangente à $ \mathscr{C}$ au point d’abscisse 1 est :
$y=f'(1)(x-1)+f(1) $
La fonction $f$ est dérivable sur $ ]0;+\infty[ $ en tant que quotient de fonctions dérivables
sur cet intervalle qui ne s’annule pas.
$f'(x)=\dfrac{\dfrac{x+1}{x}-\ln(x)}{(x+1)^2}$
Ainsi $ f'(1)=\dfrac{1}{2} et f(1)=0$.
Une équation de la tangente est donc$ y=\dfrac{x-1}{2}$.
Exercice 14:
On considère la fonction $f$ définie par $f(x)=\dfrac{1}{x\ln(x)} $.
1) Déterminer l’ensemble de définition de la fonction $ f$.
2) Déterminer les variations de la fonction $ f$.
3) Déterminer une équation de la tangente à la courbe $ \mathscr{C}$
représentant la fonction$f$au point d’abscisse$ e$.
1) La fonction \ln est définie sur $]0;+\infty[$ et s’annule en 1.
Donc la fonction$f$est définie sur $]0;1[\cup]1;+\infty[$.
2) La fonction$f$est dérivable sur $]0;1[ $et sur $]1;+\infty[$ en tant que produit et quotient de fonctions dérivables dont le dénominateur ne s’annule pas.
On va utiliser la dérivée de$ \dfrac{1}{u}$ avec $u(x)=x\ln(x)$.
$ u'(x)=\ln(x)+\dfrac{x}{x}=\ln(x)+1$.
Ainsi $ f'(x)=-\dfrac{\ln(x)+1}{\left(x\ln(x)\right)^2}$
Le signe de $ f'(x) $ dépend donc uniquement de celui de $ -\left(\ln(x)+1\right)$
$\ln(x)+1>0 \Leftrightarrow \ln(x) > -1 \Leftrightarrow x > e^{-1} $
Donc $ f'(x)<0 $ sur $]e^{-1};1[\cup]1;+\infty[$.
La fonction$f$est donc strictement croissante sur l’intervalle $ ]0;e^{-1}[$ et décroissante sur les intervalles $]e^{-1};1[$ et $]1;+\infty[$.
3) Une équation de la tangente à la courbe$ \mathscr{C}$ au point d’abscisse $e$ est :
$ y=f'(e)(x-e)+f(e) $
Or $ f'(e)=-\dfrac{\ln(e)+1}{\left(e\ln(e)\right)^2}=-\dfrac{2}{e^2}$
et$ f(e)=\dfrac{1}{e}$
Ainsi une équation de la tangente est :
$ y=-\dfrac{2}{e^2}(x-e)+\dfrac{1}{e}=-\dfrac{2x}{e^2}+\dfrac{3}{e}$
Exercice 15:
Soit la fonction g définie sur $ ]0;+\infty[ par g(x) = x – \ln x$.
Partie I
1) Étudier les variations de $g$.
2) En déduire que pour tout$ x \in ]0;+\infty[$, on a $g(x) \ge 1$.
Partie II
Soit la fonction$f$définie sur $ I = ]0;+\infty[ $ par $f(x) = \dfrac{\ln x}{x – \ln x}$.
1) Justifier que$f$est définie sur $ I$.
2) Déterminer la limite de$f$en $0 $et $+\infty$.
3) Etudier les variations de$f$et donner son tableau de variations.
4) Soient $A(0;-1) $ et $M\left(x;f(x)\right) $ pour $x > 0$.
Déterminer $m$ le coefficient directeur de la droite$ (AM) $en fonction de$ x$ puis $\lim\limits_{x \to 0^+} m$.
Interpréter graphiquement.
5) Tracer la courbe $ \mathscr{C}_f $dans le plan muni d’un repère orthonormal.
Partie I
1) $g $ est la somme de deux fonctions dérivables sur $]0;+\infty[$.
Elle est donc également dérivable sur cet intervalle.
$g'(x) = 1 – \dfrac{1}{x} = \dfrac{x – 1}{x}$
On obtient ainsi le tableau de variations suivant :
2) Cela signifie donc que $1$ est le minimum de la fonction atteint pour $x= 1$.
Par conséquent, pour tout $ x \in ]0;+\infty[, g(x) \ge 1$.
Partie II
1) La fonction $\ln$ est définie sur $]0;+\infty[$.
De plus, d’après la question A.2., $ g(x) \ge 1 $donc le dénominateur ne
s’annule jamais sur cet intervalle.
Par conséquent$f$est définie sur $I$.
2) $f(x) = \dfrac{\ln x}{\ln x \left(\dfrac{x}{\ln x} – 1\right)} = \dfrac{1}{\dfrac{x}{\ln x} – 1}$
Or $ \lim\limits_{x \to 0^+} \ln x = -\infty$ donc $\lim\limits_{x \to 0^+} \dfrac{1}{\ln x} = 0$
Par conséquent $ \lim\limits_{x \to 0^+}\dfrac{x}{\ln x} = 0$ et $\lim\limits_{x \to 0^+} \dfrac{x}{\ln x} – 1 = -1$.
Donc $ \lim\limits_{x \to 0^+} f(x) = -1$.
$f(x) = \dfrac{\ln x}{x\left(1 – \dfrac{\ln x}{x}\right)} = \dfrac{\dfrac{\ln x}{x}}{1 – \dfrac{\ln x}{x}}$.
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x} = 0$ donc $\lim\limits_{x \to +\infty} f(x) =0$.
3) La fonction $f$ est dérivable sur I en tant que somme et quotient de
fonctions dérivables sur$ I$ dont le dénominateur ne s’annule pas.
$f'(x) = \dfrac{\dfrac{1}{x}(x – \ln x) – \ln x \times \left(1 – \dfrac{1}{x}\right)}{\left(x – \ln x\right)^2} = \dfrac{1 – \ln x}{\left(x – \ln x\right)^2}$
Le signe de$ f'(x) $ ne dépend que de celui de $1 – \ln x$.
Or
$ \begin{array}{ll}1 – \ln x > 0 & \Leftrightarrow -\ln x > -1 \\& \Leftrightarrow \ln x < 1 \\& \Leftrightarrow x < e \end{array}$
$ \begin{array}{ll} m &= \dfrac{f(x) – (-1)}{x – 0} \\\\
&= \dfrac{f(x) + 1}{x} \\\\
&=\dfrac{\dfrac{\ln x}{x – \ln x} + 1}{x} \\\\
&= \dfrac{\dfrac{x}{x – \ln x}}{x} \\\\
&= \dfrac{1}{x – \ln x}\end{array}$
$\lim\limits_{x \to 0^+} \ln x = -\infty $ donc $\lim\limits_{x \to 0^+} m = 0$.
Cela signifie donc que la courbe représentative de la fonction$f$possède une demi-tangente horizontale en 0.
<
Exercice 16:
Partie A
Soit$f$la fonction définie sur l’intervalle $]-1;+\infty[$ par $f(x) = \dfrac{x}{x + 1} – 2\ln(x + 1$
1) Déterminer les variations de la fonction $ f$.
2) Déterminer les limites de$f$aux bornes de son ensemble de définition.
3) Calculer $ f(0) $.
Montrer que l’équation $f(x)= 0$ admet exactement deux solutions dont l’une, non nulle, que l’on désignera par $\alpha$.
Fournir une valeur approchée à $10^{-2}$ près de $\alpha$.
4) Etudier le signe de $f(x) $ sur $]-1;+\infty[$.
Partie B
Soit $g$ la fonction définie sur l’ensemble $]-1;0[\cup]0;+\infty[ $ par $g(x) = \dfrac{\ln(x +1)}{x^2}$
1) Déterminer les limites de $ g$ aux bornes de son ensemble de définition.
2) Calculer $ g'(x) $ et dresser le tableau de variations de la fonction $g$.
3) Montrer que $g(\alpha) = \dfrac{1}{2\alpha(\alpha + 1)} $.
En déduire une valeur approchée de$ g(\alpha) $ à $10^{-2} $près.
Partie A
1) La fonction$f$est dérivable sur$ ]-1;+\infty[$ comme somme et quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
$\begin{array}{ll} f'(x) &= \dfrac{(x + 1) – x}{(x + 1)^2} – \dfrac{2}{x + 1} \\\\
&=\dfrac{1}{(x + 1)^2} – \dfrac{2}{x + 1} \\\\
&= \dfrac{1}{(x + 1)^2} – \dfrac{2(x+1)}{(x + 1)^2} \\\\
&= \dfrac{-2x – 1}{(x + 1)^2} \end{array}$
Le signe de $ f'(x) $ ne dépend donc que de celui de $-2x – 1$.
Or $ -2x – 1 > 0 \Leftrightarrow x < – \dfrac{1}{2}$
On obtient ainsi le tableau de variations suivants.
Les limites sont déterminées à la question suivante.
2) $f(x) = \dfrac{1}{x + 1}\left(x – 2(x + 1)\ln(x+1)\right) $.
$\lim\limits_{x \to -1^+} x + 1 = 0^+ et \lim\limits_{x \to 0^+} x\ln x = 0 $
Donc $\lim\limits_{x \to -1^+} \dfrac{1}{x + 1} = +\infty $et $\lim\limits_{x \to -1^+} (x+1)\ln(x + 1) = 0$
Par conséquent $\lim\limits_{x \to -1^+} \left(x – 2(x – 2(x + 1)\ln(x + 1)\right) = -1$.
Finalement $\lim\limits_{x \to -1^+} f(x) = -\infty$.
$f\left(-\dfrac{1}{2}\right) = \dfrac{-\dfrac{1}{2}}{\dfrac{1}{2}} – 2\ln \dfrac{1}{2} =-1 + 2\ln 2$.
$\lim\limits_{x \to +\infty} \dfrac{x}{x + 1} = 1$ d’après les termes de plus haut degré.
$\lim\limits_{x \to +\infty} \ln (x + 1) = +\infty$
Donc $ \lim\limits_{x \to +\infty} f(x) = -\infty$.
3) $f(0) = 0 – 2\ln 1 = 0$.
Sur l’intervalle $ ]-1;-\dfrac{1}{2}]$, la fonction$f$est continue (car dérivable) et strictement croissante.
$f\left(-\dfrac{1}{2}\right) =-1 + 2\ln 2 > 0$
$\lim\limits_{x \to -1^+} f(x) = -\infty $
Par conséquent $ 0 \in ]-\infty;-1 + 2\ln 2[$
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation f(x) = 0 possède une unique solution $\alpha $ sur cet intervalle.
Sur l’intervalle $[-\dfrac{1}{2};+\infty[$, la fonction$f$est continue et strictement décroissante.
$f\left(-\dfrac{1}{2}\right) =-1 + 2\ln 2 > 0$
$\lim\limits_{x \to +\infty}= -\infty$
Par conséquent $ 0 \in ]-\infty;-1 + 2\ln 2[$
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation f(x) = 0 possède une unique solution sur cet intervalle.
Mais 0 appartient à cet intervalle et $f(0) = 0$.
Par conséquent l’équation $ f(x) = 0 $ possède deux solutions sur $]-1;+\infty[ $ dont l’une non nulle.
D’après le menu table de la calculatrice, on obtient$ \alpha \approx -0,72 $ à $10^{-2}$ près.
4) Puisque la fonction$f$est strictement croissante sur$ ]-1;-\dfrac{1}{2}] $
et décroissante sur$ [-\dfrac{1}{2};+\infty[$, on obtient le tableau de signes suivant :
Partie B
1) $\lim\limits_{x \to -1^+} \ln(x + 1) = -\infty$ et $\lim\limits_{x \to -1^+} x^2 = 1$
Donc $\lim\limits_{x \to -1^+} g(x) = -\infty$
$g(x) = \dfrac{\ln(x + 1)}{x} \times \dfrac{1}{x}$
Or $ \lim\limits_{x \to 0} \dfrac{\ln(x + 1)}{x} = 1$ , $\lim\limits_{x \to 0^-} \dfrac{1}{x} = -\infty $ et $ \lim\limits_{x \to 0^+} \dfrac{1}{x} = +\infty$
Par consequent $\lim\limits_{x \to 0^-} g(x) = -\infty$ et $\lim\limits_{x \to 0^+} g(x) = +\infty$
$g(x) = \dfrac{\ln(x + 1)}{x + 1} \times \dfrac{x + 1}{x^2}$
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x} = 0$
Donc $\lim\limits_{x \to +\infty} \dfrac{\ln(x+1)}{x+1} = 0$
$\lim\limits_{x \to +\infty} \dfrac{x+1}{x^2} = 0$
d’après la limite des termes de plus haut degré.
Finalement $\lim\limits_{x \to +\infty} g(x) = 0$
2) g est dérivable sur $]-1;0[\cup]0;+\infty[$ comme somme et quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
$g'(x) = \dfrac{\dfrac{x^2}{x+1} – 2x\ln(x + 1)}{x^4} = \dfrac{f(x)}{x^3}$
D’après la question A.4 on obtient le tableau de variations suivant :
3) $f(\alpha) = 0$ par conséquent $\dfrac{\alpha}{\alpha + 1} – 2\ln(\alpha + 1) = 0$
soit $ \ln(\alpha + 1) = \dfrac{\alpha}{2(\alpha + 1)} $.
Ainsi $ g(\alpha) = \dfrac{\dfrac{\alpha}{2(\alpha + 1)}}{\alpha^2} = \dfrac{1}{2\alpha(\alpha + 1)} $.
En utilisant la valeur approchée trouvée à la question A.3 on obtient $g(\alpha) \approx -2,48$.
Exercice 17:
Résoudre dans $ \mathbb{R}$ le système $\begin{cases} \ln x – \ln y = 1\\\\x + y = 2e \end{cases}$
Les couples solutions ne pourront contenir que des réels strictement positifs.
$\begin{array}{ll} \begin{cases} \ln x – \ln y = 1\\\\x + y = 2e \end{cases} &\Leftrightarrow \begin{cases} \ln \dfrac{x}{y} = \ln e \\\\x + y = 2e \end{cases} \\\\
&\Leftrightarrow \begin{cases} \dfrac{x}{y}= e\\\\x + y = 2e \end{cases} \\\\
&\Leftrightarrow \begin{cases} x = y e \\\\x + y = 2e \end{cases} \\\\
&\Leftrightarrow \begin{cases} x= y e\\\\y e + y = 2e \end{cases} \\\\
&\Leftrightarrow \begin{cases} x= y e\\\\y (1 + e) = 2e \end{cases} \\\\
&\Leftrightarrow \begin{cases} x= y e\\\\y = \dfrac{2e}{1 + e} \end{cases} \\\\
&\Leftrightarrow \begin{cases} x= \dfrac{2e^2}{1 + e}\\\\y = \dfrac{2e}{1 + e} \end{cases}
\end{array}$
La solution du système est donc $ \left( \dfrac{2e^2}{1 + e};\dfrac{2e}{1 + e} \right) $.
Exercice 18:
On considère l’équation $(E_1) $ :
$e^x – x^n = 0$
où $x $ est un réel strictement positif et $n $ un entier naturel non nul.
1) Montrer que l’équation $ (E_1) $ est équivalente à l’équation $(E_2) $:
$\ln(x) – \dfrac{x}{n} = 0$.
2) Pour quelles valeurs de$ n$ l’équation $(E_1) $ admet-elle deux solutions?
1)
$\begin{array}{ll} e^x – x^n = 0 &\Leftrightarrow \text{e}^x=x^n \\\\
&\Leftrightarrow x = n \ln (x) \\\\
&\Leftrightarrow \ln(x) = \dfrac{x}{n} \\\\
&\Leftrightarrow \ln(x) – \dfrac{x}{n} = 0 \end{array}$
2) Soit $ f_n$ la fonction définie sur $]0;+\infty[ $ par $f_n(x)=\ln(x) – \dfrac{x}{n}$.
Cette fonction est dérivable sur $ ]0;+\infty[$ en tant que
somme de fonctions dérivables sur cet intervalle.
$f_n'(x) = \dfrac{1}{x} – \dfrac{1}{n}$.
$f_n'(x) >0 \Leftrightarrow x < n$.
On obtient ainsi le tableau de variations suivant :
$\lim\limits_{x \to 0} \ln(x) = -\infty$ donc $\lim\limits_{x \to 0} f_n(x) = -\infty$
$f(x) = x\left(\dfrac{\ln(x)}{x} – \dfrac{1}{n} \right) $.
Or $\lim\limits_{x \to +\infty} \dfrac{\ln(x)}{x} = 0$ donc $\lim\limits_{x \to +\infty} f_n(x) = -\infty$.
$\ln n -1 > 0 \Leftrightarrow n > \text{e}$.
Par conséquent si$ n \le 2, f_n(x) < 0$ et l’équation $(E_2) $ n’aura pas de solution.
Si $ n \ge 3$, la fonction $f_n$ est dérivable sur $]0;+\infty[$ donc continue .
Sur $ ]0;n[ $ la fonction est strictement croissante.
$\lim\limits_{x \to 0} f_n(x) =-\infty et f_n(n) >0$.
D’après le théorème de la bijection (ou le corollaire du théorème des valeurs intermédiaires) l’équation $ f_n(x) = 0 $ possède une unique solution.
Sur$ ]n;+\infty[$, la fonction $ f_n$ est strictement décroissante.
$f_n(n) >0 $et $\lim\limits_{x \to +\infty} f_n(x) = -\infty$.
D’après le théorème de la bijection l’équation $f_n(x)=0 $ possède une unique solution.
Par conséquent l’équation $(E_2) $, et donc $(E_1) $ possède deux solutions si, et seulement si, $ n \ge 3$








Commentaires
Enregistrer un commentaire