Exercices – Généralités sur les fonctions

Exercice 1

On considère la fonction $f$ définie par $f(x)=2x+5$

1. Déterminer les images de $-1$ et de $3$.
   $\quad$
2. Calculer $f(2)$ et $f(-3)$.
   $\quad$
3. Déterminer le ou les antécédent(s) de $4$ et de $0$.

Correction Exercice 1

1. On veut donc calculer :
   $f(-1) = -2 + 5 = 3$ $\qquad$ $f(3) = 6 + 5 = 11$
   $\quad$
2. $f(2) = 4 + 5 = 9$ $\qquad$ $f(-3) = -6 + 5 = -1$
   $\quad$
3. On cherche la ou les valeurs de $x$ telles que $f(x) = 4$ soit $2x+5 = 4$ d’où $2x=-1$ et $x = -\dfrac{1}{2}$.
   L’antécédent de $4$ est $-\dfrac{1}{2}$
   $\quad$
   On cherche maintenant les valeurs de $x$ telles que $f(x) = 0$ soit $2x+5 = 0$ d’où $x= – \dfrac{5}{2}$

$\quad$

Exercice 2

Voici la courbe représentative d’une fonction $f$.

Vous fournirez, si nécessaire, des valeurs approchées au dixième.

 

1. Déterminer graphiquement une valeur approchée de $f(1)$ et  de $f(0)$.
   $\quad$
2. Déterminer graphiquement le ou les antécédent(s) de $0,5$, de $2$ et de $-1$.
   $\quad$
3. Déterminer l’ensemble de définition de $f$.

Correction Exercice 2

1. $f(1) = 0$ et $f(0) \approx 1,2$
   
2. Les antécédents de $0,5$ sont (environ) : $-1,9$ ; $0,4$ ; $1,7$ et $2,8$
   $\quad$
   Les antécédents de $2$ sont (environ) : $-1,7$ et $-0,4$.
   $\quad$
   $-1$ n’a pas d’antécédent par $f$.
   
3. La fonction $f$ est définie sur $[-2;3]$

$\quad$

Exercice 3

On considère la fonction $f$ définie par $f(x)= \dfrac{2 x – 3}{x-1}$.

1. Pour quelle valeur de $x$ la fonction $f$ n’est-elle pas définie?
   $\quad$
2. Déterminer $f(0)$, $f(-1)$ et $f\left(-\dfrac{1}{2} \right)$.
   $\quad$
3. Déterminer les antécédents de $0$; $1$ et $-2$.

Correction Exercice 3

1. $f$ n’est pas définie pour la valeur de $x$ qui annule son dénominateur.
   Or $x-1 = 0 \Leftrightarrow x=1$
   $f$ n’est donc pas définie en $1$.
   $\quad$
2. $f(0) = \dfrac{-3}{-1} = 3$ $\qquad$ $f(-1) = \dfrac{-2 – 3}{-1 – 1} = \dfrac{5}{2}$
   $\quad $
   $f\left(-\dfrac{1}{2} \right) = \dfrac{-1 – 3}{-\dfrac{1}{2} – 1} = \dfrac{-4}{-\dfrac{3}{2}} = -4 \times \dfrac{-2}{3} = \dfrac{8}{3}$
   $\quad$
3. On cherche à résoudre :
   $f(x) = 0$ soit $\dfrac{2 x – 3}{x – 1} = 0$ par conséquent $2 x – 3 = 0$ donc $x = \dfrac{3}{2}$.
   L’antécédent de $0$ est $\dfrac{3}{2}$
   $\quad$
   $f(x) = 1$ soit $\dfrac{2 x – 3}{x – 1} = 1$ par conséquent $2 x – 3 = x – 1$ donc $x = 2$ .
   L’antécédent de $1$ est $2$
   $\quad$
   $f(x) = -2$ soit $\dfrac{2 x – 3}{x – 1} = -2$ par conséquent $2 x – 3 = -2(x – 1)$ ce qui nous amène à $2x -3 = -2x + 2$  soit $4x = 5$.
   L’antécédent de $-2$ est $\dfrac{5}{4}$.

$\quad$

Exercice 4

On considère la fonction $f$ définie par $f(x) = – \dfrac{1}{2}x^2+2x -1$.

Compléter le tableau de valeurs suivant.

$$\begin{array}{|c|c|c|c|c|c|c|}
\hline
x & -2 & -1 & 0~ & 1~ & 2~ & 3~ \\\\
\hline
f(x) & & & & & & \\\\
\hline
\end{array}$$

Correction Exercice 4

$$\begin{array}{|c|c|c|c|c|c|c|}
\hline
x & -2 & -1 & 0~ & 1~ & 2~ & 3~ \\\\
\hline
f(x) & -7& -\dfrac{7}{2} &-1 & \dfrac{1}{2} & 1  & \dfrac{1}{2} \\\\
\hline
\end{array}$$

$\quad$

Exercice 5

1. Dans chacun des cas, représenter sur une droite graduée l’appartenance à l’intervalle.
   a. $x \in ]2;6[$.
   $\quad$
   b. $x\in ]-\infty;1]$
   $\quad$
   c. $x\in ]5;+\infty[$
   $\quad$
2. Traduire chaque inégalité sous la forme de l’appartenance à un intervalle.
   a. $-2<x \le 3$
   $\quad$
   b. $3>x$
   $\quad$
   c. $1 \le x$

Correction Exercice 5

1. $\quad$
   
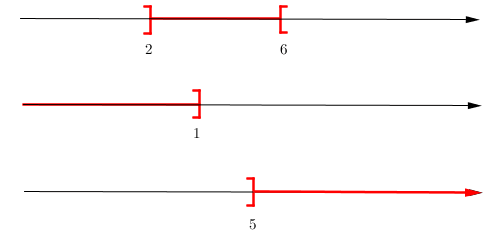
2. a. Si $-2<x \le 3$ alors on a  $x \in ]-2;3]$
   $\quad$
   b. Si $3>x$ alors on a $x \in ]-\infty;3[$
   $\quad$
   c. Si $1 \le x$ alors on a $x  \in [1;+\infty[$

Exercice 6

Soit $f$ la fonction définie par $f(x) = 2x^2$.

1. Que peut-on dire de l’ensemble de définition de $f$?
   Calculez les images par $f$ des réels $0$; $\sqrt{2}$; $-4$.
   $\quad$
2. Vérifiez que $4$ a deux antécédents par $f$.
   $\quad$
3. Pourquoi $-4$ n’est-il l’image d’aucun réel?
   $\quad$
4. Quels sont les réels qui ont $\dfrac{5}{4}$ pour image par $f$?

Correction Exercice 6

1. Pour tout nombre réel $x$, $x^2$ existe. Par conséquent la fonction $f$ est définie sur $\R$.
   $\quad$
   $f(0) = 2 \times 0^2 = 0$ $\quad$ $f\left(\sqrt{2}\right) = 2 \times 2 = 4$ $\quad$ $f(-4) = 2 \times (-4)^2 = 32$.
   $\quad$
2. On cherche à résoudre $f(x) = 4$ soit $2x^2 = 4$ et donc $x^2 = 2$.
   Cette équation possède deux solutions : $-\sqrt{2}$ et $\sqrt{2}$.
   $\quad$
3. Pour tout réel $x$, $2x^2 \ge 0$. Par conséquent $-4$ n’a pas d’antécédent par $f$.
   $\quad$
4. On veut résoudre $2x^2 = \dfrac{5}{4}$ soit $x^2 = \dfrac{5}{8}$.
   Cette équation possède deux solutions : $-\sqrt{\dfrac{5}{8}}$ et $\sqrt{\dfrac{5}{8}}$.

$\quad$

Exercice 7

Soit $f$ la fonction définie sur $\R$ par $f(x)=(2x + 6) – (x+3)^2$.

1. Développez puis factorisez $f(x)$.
   $\quad$
2. En choisissant l’expression la mieux adaptée, calculez à la main les images de $0$, $\sqrt{2}$ et $-1$.
   $\quad$
3. Déterminez par le calcul le ou les antécédents de $0$ et $-3$ par $f$.

Correction Exercice 7

1. $f(x) = 2x+6 – (x^2 + 6x + 9) = -x^2 – 4x – 3$
   $\quad$
   $f(x) = 2(x + 3) – (x+3)^2 = (x+3) \left[ 2 – (x+3) \right] = (x+3)(-x -1)$
   $\quad$
2.  $f(0) = -0^2 – 4 \times 0 – 3 = -3$
   $\quad$
   $f\left(\sqrt{2} \right) = -2 – 4\sqrt{2} – 3 = -5 -4\sqrt{2}$
   $\quad$
   $f(-1) = (-1 + 3)(1 – 1) = 0$
   $\quad$
3. On veut résoudre l’équation $(x+3)(-x – 1) = 0$.
   Un produit de facteurs est nul si, et seulement si, l’un de ses facteurs au moins est nul. On résout donc les équations suivantes :
   $x+3 = 0$ ou $-x -1 = 0$
   $x=-3$ ou $x=-1$
   $0$ possède donc deux antécédents $-3$ et $-1$.
   $\quad$
   On veut résoudre l’équation $-x^2 – 4x – 3 = -3$ soit $-x^2 – 4x = 0$ et donc $-x(x + 4) = 0$.
   Un produit de facteurs est nul si, et seulement si, l’un de ses facteurs au moins est nul. On résout donc les équations suivantes :
   $x = 0$ ou $x + 4 = 0$
   $x= 0$ ou $x= -4$.
   $-3$ possède donc deux antécédents $0$ et $-4$.

$\quad$

Exercice 8

On considère la fonction $f$ définie sur $[-2;2]$ par $f(x) = \dfrac{x^2}{x+5}$.

Les points suivants sont-ils sur la courbe représentative de $f$?

$O(0;0)$ ; $A\left(1;\dfrac{1}{6} \right)$ ; $B\left(3;\dfrac{1}{4} \right)$ ; $C\left(-2;\dfrac{4}{7} \right)$ ; $D\left(-3;\dfrac{9}{2} \right)$

Correction Exercice 8

Pour chaque point $M(x;y)$ on va regarder si $y=f(x)$

$f(0) = \dfrac{0^2}{0+5} = 0$ donc $O$ appartient à la courbe représentative de $f$.
$\quad$

$f(1) = \dfrac{1}{1+5} = \dfrac{1}{6}$ donc $A$ appartient à la courbe représentative de $f$.
$\quad$

$\dfrac{9}{3 + 5} = \dfrac{9}{8} \ne \dfrac{1}{4}$ donc $B$ n’appartient pas à la courbe représentative de $f$.
Remarque : On pouvait également dire que $3$ n’appartient pas à l’ensemble de définition de la fonction $f$; on ne pouvait donc pas parler de $f(3)$.
$\quad$

$f(-2) = \dfrac{4}{-2 + 5} = \dfrac{4}{3} \ne \dfrac{4}{7}$ donc $C$ n’appartient pas à la courbe représentative de $f$.
$\quad$

La fonction $f$ est définie sur l’intervalle $[-2;2]$. L’abscisse du point $D$ étant $-3$, celui-ci ne peut pas appartenir à la courbe représentative de $f$.
Remarque : On a pourtant $\dfrac{(-3)^2}{-3+5}=\dfrac{9}{2}$.
$\quad$

$\quad$

Exercice 9

On considère la fonction $g$ définie sur $[-4;2]$ par $g(x) = -\dfrac{1}{4}x^2+3$.

1. Remplir le tableau de valeurs suivant :
   $$\begin{array}{|c|c|c|c|c|c|c|c|}
   \hline
   x&-4&-3&-2&-1&~0&~1&~2\\
   \hline
   g(x)& & & & & & &\\
   \hline
   \end{array}$$
   $\quad$
2. Représenter sur votre feuille la courbe représentative de la fonction $f$ (on choisira un repère orthogonal $(O;I,J)$ tel que $OI = OJ = 4$ cm).
   $\quad$
3. A l’aide du graphique, déterminez une valeur approchée :
   a. des images de $1,5$ et $-1,5$.
   $\quad$
   b. du ou des antécédents de $-\dfrac{1}{2}$.
   $\quad$
4. Retrouvez les résultats par le calcul.

Correction Exercice 9

1. $\quad$
   $$\begin{array}{|c|c|c|c|c|c|c|c|}
   \hline
   x&-4&-3&-2&-1&~0&~1&~2\\
   \hline
   g(x)&-1 &0,75 &2 &2,75 &3 &2,75&2 \\
   \hline
   \end{array}$$
   $\quad$
2. Attention à l’échelle demandée : $OI = OJ = 4$ cm
   
3. a. Graphiquement on constate que $f(-1,5) \approx 2,5$ et $f(-1,5) \approx 2,5$
   $\quad$
   b. $-\dfrac{1}{2}$ ne possède qu’un seul antécédent qui est environ égal à $-3,75$
   $\quad$
4. a. $f(1,5) = – \dfrac{1}{2} \times 1,5^2 + 3 = – \dfrac{2,25}{4} + 3 = \dfrac{39}{16}$
   $f(-1,5) = – \dfrac{1}{2} \times (-1,5)^2 + 3 = – \dfrac{2,25}{4} + 3 = \dfrac{39}{16}$
   $\quad$
   b. On veut résoudre $-\dfrac{1}{4}x^2 + 3 = -\dfrac{1}{4}$ soit $-x^2  + 12 = -1$ donc $x^2 = 13$.
   Sur $[-4;2]$, cette équation ne possède qu’une seule solution $-\sqrt{13}$.

$\quad$

Exercice 10

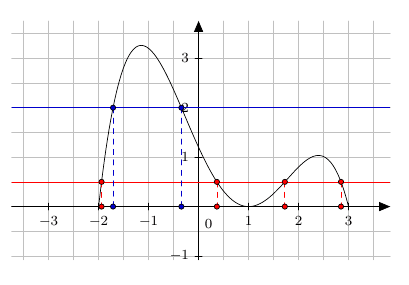
Soit $f$ une fonction dont la courbe représentative $\mathscr{C}$ est donnée ci-dessous :

En utilisant le graphique, répondre aux questions suivantes en justifiant votre démarche.

1. Déterminer l’image de $2$ par $f$.
   $\quad$
2. Déterminer $f(0)$, $f(1)$ et $f(-2)$.
   $\quad$
3. Résoudre $f(x) = -2$.
   $\quad$
4. Déterminez les antécédents de $2$ par $f$.
   $\quad$
5. Résoudre $f(x) \le 2$.
   $\quad$
6. Résoudre $f(x) > 0$.

Correction Exercice 10

1. $f(2) = 2$
   $\quad$
2. $f(0) = 0$ $\quad$ $f(1) = -2$ et $f(-2) = -2$.
   $\quad$
3. L’équation $f(x) = -2$ possède deux solutions : $-2$ et $1$.
   $\quad$
4. Les antécédents de $2$ sont : $-1$ et $2$.
   $\quad$
5. La solution de l’inéquation $f(x) \le 2$  est $]-\infty;2]$.
   $\quad$
6. La solution de l’inéquation $f(x) > 0$ est environ $]-1,75;0[\cup]1,75;+\infty[$.

Exercice 11

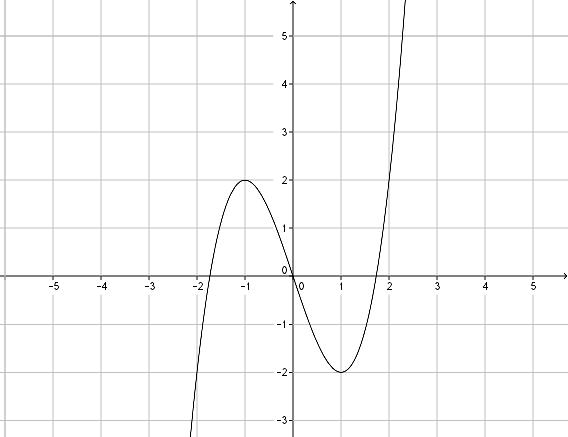
La courbe ci-dessous représente une fonction $f$.

 

1. Déterminer son ensemble de définition.
   $\quad$
2. Donner le tableau de variations de la fonction $f$.
   $\quad$
3. Quel est le maximum de la fonction $f$ sur :
   a. son ensemble de définition
   $\quad$
   b. $[-3;2]$
   $\quad$
4. Quel est le minimum de la fonction $f$ sur :
   a. son ensemble de définition
   $\quad$
   b. $[2;4]$
   $\quad$

Correction Exercice 11

1. L’ensemble de définition de la fonction $f$ est $\mathscr{D}_f = [-3;4]$.
   $\quad$
2. $\quad$
   
3. a. Son maximum sur $[-3;4]$ est $3$ atteint pour $x= 4$.
   $\quad$
   b. Son maximum sur $[-3;2]$ est $2$ atteint pour $x= -3$.
   $\quad$
4. a. Son minimum sur $[-3;4]$ est $-2$ atteint pour $x = 0$.
   $\quad$
   b. Son minimum sur $[2;4]$ est $0$ atteint pour $x= 2$.

$\quad$

Exercice 12

Indiquez les erreurs dans les tableaux de variation suivants :

Tableau 1

 

Tableau 2

 

Correction Exercice 12

Tableau 1 : La fonction en peut pas décroitre de la valeur $-1$ à la valeur $1$.  Elle ne peut pas croitre de la valeur $1$ à la valeur $\dfrac{4}{5}$. Elle ne peut pas non plus décroitre de la valeur $\dfrac{4}{5}$ à la valeur $2$.

Tableau 2 : $\dfrac{7}{2}$ n’est pas compris entre $-3$ et $2$. La fonction ne peut pas croitre de $3$ à $2$.

$\quad$

Exercice 13

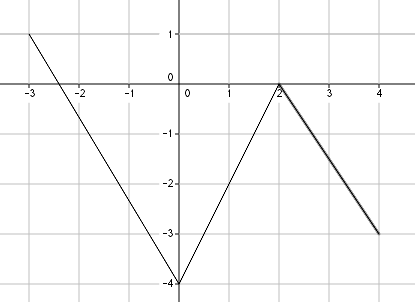
Voici le tableau de variation d’une fonction $g$ définie sur l’intervalle $[-3;4]$.

1. Décrire les variations de la fonction$g$.
   $\quad$
2. Comparer lorsque cela est possible :
   • $g(-3)$ et $g(-1)$
   • $g(1)$ et $g(3)$
   $\quad$
3. Lire le maximum de $g$ sur $[0;4]$ et le minimum de $g$ sur $[-3;4]$.
   $\quad$
4.  Tracer une courbe susceptible de représenter graphiquement la fonction $g$.

Correction Exercice 13

1. La fonction $g$ est décroissante sur les intervalles $[-3;0]$ et $[2;4]$ et croissante sur $[0;2]$.
   $\quad$
2. $-3$ et $-1$ appartiennent tous les deux à l’intervalle $[-3;0]$ sur lequel la fonction $g$ est décroissante.
   Par conséquent $g(-3) > g(-1)$.$\quad$
   $1$ et $3$ n’appartiennent pas à un intervalle sur lequel la fonction $g$ est monotone. On ne peut donc pas comparer leur image.
   $\quad$
3. Le maximum de la fonction $g$ sur  $[0;4]$ est $0$. Il est atteint pour $x=2$.
   $\quad$
   Le minimum de la fonction $g$ sur $[-3;4]$ est $-4$. Il est atteint pour $x= 0$.
4. Une représentation possible (il en existe une infinité) est :
   

Exercice 14

Tracer une courbe susceptible de représenter une fonction $f$ sachant que :

• $f$ est définie sur l’intervalle $[-5;4]$;
• $f$ admet un minimum $–3$ et un maximum $5$ qui ne sont atteints ni en $–5$ ni en $4$;
• l’image de $–5$ est négative;
• $0$ possède trois antécédents.

$\quad$

Correction Exercice 14

Voici une proposition (il en existe une infinité).

$\quad$

Exercice 15

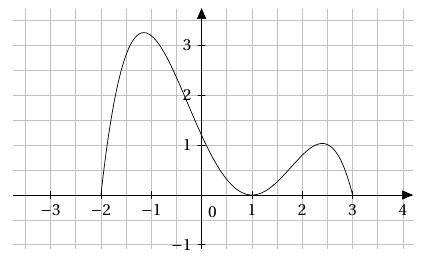
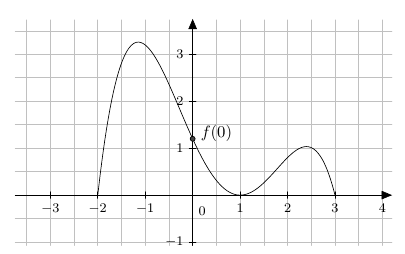
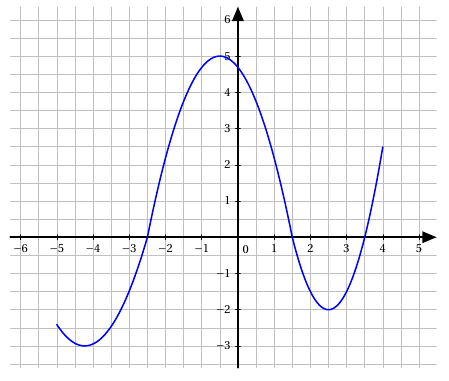
On considère une fonction $f$ dont la représentation graphique est donnée ci-dessous.

1. Déterminer l’ensemble de définition $\mathscr{D}_f$ de la fonction $f$.
   $\quad$
2. Déterminer le tableau de variation de la fonction $f$.
   $\quad$
3. Préciser le minimum et le maximum de $f$ sur $\mathscr{D}_f$ et pour quelles valeurs sont-ils atteints?
   $\quad$

Correction Exercice 15

1. La fonction $f$ est définie sur $\mathscr{D}_f=[-2;6]$.
   $\quad$
2. Le tableau de variation de la fonction $f$ est :
   
3. Le minimum de la fonction $f$ sur $\mathscr{D}_f$ est $-4$. Il est atteint en $-1$ et $3$.
   Le maximum de la fonction $f$ sur $\mathscr{D}_f$ est $5$. Il est atteint en $6$.
   $\quad$

$\quad$

Exercice 16

On considère une fonction $f$ dont le tableau de variation est :

1. Quel est l’ensemble de définition $\mathscr{D}_f$ de la fonction $f$?
   $\quad$
2. Préciser le minimum et le maximum de la fonction $f$ sur $\mathscr{D}_f$.
   $\quad$
3. Préciser le minimum et le maximum de la fonction $f$ sur l’intervalle $[-10;9]$.
   $\quad$
4. Compléter le plus précisément possible les inégalités suivantes :
   $\quad$
   a. $\ldots \ldots \pp f(-5) \pp \ldots \ldots$
   $\quad$
   b. $\ldots \ldots \pp f(20)\pp \ldots \ldots$
   $\quad$

Correction Exercice 16

1. La fonction $f$ est définie sur $\mathscr{D}_f=[-10;30]$.
   $\quad$
2. Le minimum de la fonction $f$ sur l’intervalle $[-10;30]$ est $-52$.
   Le maximum de la fonction $f$ sur l’intervalle $[-10;30]$ est $33$.
   $\quad$
3. Le minimum de la fonction $f$ sur l’intervalle $[-10;9]$ est $-25$.
   Le maximum de la fonction $f$ sur l’intervalle $[-10;9]$ est $33$.
   $\quad$
4. a. $-25 \pp f(-5) \pp 33$
   $\quad$
   b. $-52 \pp f(20)\pp 20$
   $\quad$

$\quad$

Exercice 17

On considère une fonction $f$ dont le tableau de variation est le suivant :

1. Quel est l’ensemble de définition de la fonction $f$?
   $\quad$
2. a. Quel est le maximum de la fonction $f$ sur l’intervalle $]-\infty;10]$?
   $\quad$
   b. Quel est le signe de $f(x)$ sur l’intervalle $]-\infty;10]$?
   $\quad$
3. a. Quel est le maximum de la fonction $f$ sur $\R$?
   $\quad$
   b. En déduire le nombre de solution de l’équation $f(x)=2$.
   $\quad$

Correction Exercice 17

1. La fonction $f$ est définie sur $\R$.
   $\quad$
2. a. Le maximum de la fonction $f$ sur l’intervalle $]-\infty;10]$ est $0$.
   $\quad$
   b. Sur l’intervalle $]-\infty;10]$ le maximum est $0$. On a donc $f(x)\pp 0$ pour tout réel $x\in]-\infty;10]$.
   $f(x)$ est donc négatif ou nul sur cet intervalle.
   $\quad$
3. a. Le maximum de la fonction $f$ sur $\R$ est $\dfrac{13}{7}$.
   $\quad$
   b. Par conséquent, pour tout réel $x$, on a $f(x)\pp \dfrac{13}{7}<2$.
   $2$ ne possède donc pas d’antécédent par la fonction $f$ et l’équation $f(x)=2$ ne possède pas de solution sur $\R$.
   $\quad$

$\quad$

Exercice 18

On considère une fonction $f$ définie sur l’intervalle $[-4;5]$ dont le tableau de variation est donné ci-dessous.

Les affirmations suivantes sont-elles vraies ou fausses? Justifier votre réponse.

Affirmation 1 : $f(4)\pg 0$.

$\quad$

Affirmation 2 : La courbe représentant la fonction $f$ coupe l’axe des abscisses en un seul point.

$\quad$

Correction Exercice 18

D’après le tableau de variation on sait que $-2 \pp f(4) \pp 1$.
On ne peut donc pas déterminer le signe de $f(4)$.
Affirmation 1 fausse

D’après le tableau de variation on sait que $f(-1)=0$. La courbe représentant la fonction $f$ coupe donc l’axe des abscisses au point d’abscisses $-1$.
On sait également que la fonction $f$ est strictement décroissante sur l’intervalle $[3;5]$ et qu’elle prend des valeurs comprises entre $-2$ et $1$. Elle prendra donc une nouvelle fois sur cet intervalle (il faudra attendre la terminale pour avoir une justification précise) la valeur $0$.
Affirmation 2 fausse

$\quad$

$\quad$

Exercice 19

On considère une fonction $f$ dont le tableau de variation est donné ci-dessous :

1. Quel est l’ensemble de définition de la fonction $f$?
   $\quad$
2. Combien d’antécédents le nombre $5$ possède-t-il par la fonction $f$ sur son ensemble de définition?
   $\quad$
3. Compléter le plus précisément possible les inégalités suivantes :
   $\quad$
   a. $\ldots \ldots \pp f(3) \pp \ldots \ldots$
   $\quad$
   b. $\ldots \ldots \pp f(-2) \pp \ldots \ldots$
   $\quad$

Correction Exercice 19

1. L’ensemble de définition de la fonction $f$ est $\mathscr{D}_f=[-10;+\infty[$.
   $\quad$
2. Sur l’intervalle $[-10;0]$ le maximum de la fonction $f$ est $1$. Par conséquent $5$ ne possède pas d’antécédent sur cet intervalle.
   Sur l’intervalle $[0;+\infty[$ le maximum de la fonction $f$ est $5$, atteint pour $x=2$. Par conséquent $5$ possède un unique antécédent sur cet intervalle.
   Le nombre $5$ possède donc un unique antécédent par la fonction $f$ sur $\mathscr{D}_f$.
   $\quad$
3. a. $-1 \pp f(3) \pp 5$
   $\quad$
   b. $-7 \pp f(-2) \pp 1$
   $\quad$

Exercice 20

Dans chacun des cas, déterminer le tableau de signe de la fonction $f$ donc une représentation graphique a été donnée.

$\quad$

Correction Exercice 20

On utilise la propriété suivante :

 Propriété : On considère une fonction $f$ et sa représentation graphique $\mathscr{C}_f$.

• Sur l’intervalle $[a,b]$ on a $f(x)>0 \ssi$ la courbe $\mathscr{C}_f$ est au-dessus de l’axe des abscisses sur l’intervalle $[a;b]$.
• Sur l’intervalle $[a,b]$ on a $f(x)<0 \ssi$ la courbe $\mathscr{C}_f$ est au-dessous de l’axe des abscisses sur l’intervalle $[a;b]$
• $f\left(x_0\right)=0 \ssi$ la courbe $\mathscr{C}_f$  coupe l’axe des abscisses au point d’abscisse $x_0$.

On obtient alors les tableaux de signes suivants :

$\quad$

$\quad$

$\quad$

Exercice 21

Déterminer, par le calcul, le signe des fonctions suivantes définies sur $\R$ :

1. $f:x\mapsto x+5$
   $\quad$
2. $g:x\mapsto 2x-3$
   $\quad$
3. $h:x\mapsto -4x+1$
   $\quad$
4. $i:x\mapsto \dfrac{1}{2}x+4$
   $\quad$
5. $j:x\mapsto -\dfrac{2}{3}x+7$
   $\quad$

Correction Exercice 21

1. 1. On a $f(x)=x+5$.
      $f(x)=0 \ssi x+5=0 \ssi x=-5$
      et
      $f(x)>0 \ssi x+5>0 \ssi x>5$
      On obtient donc le tableau de signes suivant :
      
      $\quad$
   2. On a $g(x)=2x-3$
      $g(x)=0 \ssi 2x-3=0 \ssi 2x=3 \ssi x=1,5$
      et
      $g(x)>0 \ssi 2x-3>0 \ssi 2x>3 \ssi x>1,5$
      On obtient donc le tableau de signes suivant :
      
      $\quad$
   3. On a $h(x)=-4x+1
      $h(x)=0 \ssi -4x+1=0 \ssi -4x=-1 \ssi x=0,25$
      et
      $h(x)>0 \ssi -4x+1>0 \ssi -4x>-1 \ssi x<0,25$
      (on divise la dernière inégalité par un nombre négatif)
      On obtient donc le tableau de signes suivant :
      
      $\quad$
   4. On a $i(x)=\dfrac{1}{2}x+4$
      $i(x)=0 \ssi \dfrac{1}{2}x+4= 0 \ssi \dfrac{1}{2}x=-4 \ssi x=-8$
      et
      $i(x)>0 \ssi \dfrac{1}{2}x+4> 0 \ssi \dfrac{1}{2}x>-4 \ssi x>-8$
      On obtient donc le tableau de signes suivant :
      
      $\quad$
   5. On a $j(x)=-\dfrac{2}{3}x+7$
      $j(x)=0 \ssi -\dfrac{2}{3}x+7=0 \ssi -\dfrac{2}{3}x=-7 \ssi x=10,5$
      et
      $j(x)>0 \ssi -\dfrac{2}{3}x>7=0 \ssi -\dfrac{2}{3}x>-7 \ssi x<10,5$
      (on divise la dernière inégalité par un nombre négatif)
      On obtient donc le tableau de signes suivant :
      

1. $\quad$

 

Exercice 22

Déterminer graphiquement les solutions des inéquations suivantes :

$\quad$

Correction Exercice 22

1. L’ensemble solution est : $]-4;4[$.
   $\quad$
2. L’ensemble solution est ,environ : $]-\infty;-3,8]\cup[1,8;+\infty[$.
   $\quad$
3. L’ensemble solution est : $]-1;3[$.
   $\quad$

A