Inéquations – Tableaux de signes
Inéquations – Tableaux de signes
1) $2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x =-\dfrac{1}{2}$
$x-3 > 0 \Leftrightarrow x > 3$
$x-3 = 0 \Leftrightarrow x = 3$
2) $x-2> 0 \Leftrightarrow x > 2$
$x-2= 0 \Leftrightarrow x = 2$
$x-5 > 0 \Leftrightarrow x > 5$
$x-5 = 0 \Leftrightarrow x = 5$
3) $3x-5 > 0 \Leftrightarrow 3x > 5 \Leftrightarrow x > \dfrac{5}{3}$
$3x-5 = 0 \Leftrightarrow 3x = 5 \Leftrightarrow x = \dfrac{5}{3}$
$-2-x > 0 \Leftrightarrow -x > 2 \Leftrightarrow x < -2$
$-2-x = 0 \Leftrightarrow -x = 2 \Leftrightarrow x = -2$
4) $-5x+1>0 \Leftrightarrow -5x>-1 \Leftrightarrow x<\dfrac{1}{5}$
$-5x+1=0\Leftrightarrow -5x=-1 \Leftrightarrow x=\dfrac{1}{5}$
$3-4x>0\Leftrightarrow -4x>-3 \Leftrightarrow x<\dfrac{3}{4}$
$3-4x=0 \Leftrightarrow -4x=-3 \Leftrightarrow x=\dfrac{3}{4}$
5) $4x+7>0 \Leftrightarrow 4x>-7 \Leftrightarrow x>-\dfrac{7}{4}$
$4x+7=0 \Leftrightarrow 4x=-7 \Leftrightarrow x=-\dfrac{7}{4}$
$5-3x>0 \Leftrightarrow -3x>-5 \Leftrightarrow x<\dfrac{5}{3}$
$5-3x=0 \Leftrightarrow -3x=-5 \Leftrightarrow x=\dfrac{5}{3}$
1) $3x + 1 > 0 \Leftrightarrow 3x > -1\Leftrightarrow x > -\dfrac{1}{3}$
$3x + 1 = 0 \Leftrightarrow 3x = -1\Leftrightarrow x = -\dfrac{1}{3}$
$2x + 3 > 0 \Leftrightarrow 2x > -3 \Leftrightarrow x > -\dfrac{3}{2}$
$2x + 3 = 0 \Leftrightarrow 2x = -3 \Leftrightarrow x = -\dfrac{3}{2}$
On cherche à résoudre l’inéquation $(3x + 1)(2x + 3) > 0$.
Par conséquent la solution est $\left]-\infty;-\dfrac{3}{2}\right[\cup\left]-\dfrac{1}{3};+\infty\right[$.
2) $x-3 > 0 \Leftrightarrow x > 3$
$x-3 = 0 \Leftrightarrow x = 3$
$4+x > 0 \Leftrightarrow x > -4$
$4+x = 0 \Leftrightarrow x = -4$
On cherche à résoudre l’inéquation $(x-3)(4 + x) > 0$.
Par conséquent la solution est $]-\infty;-4]\cup[3;+\infty[$.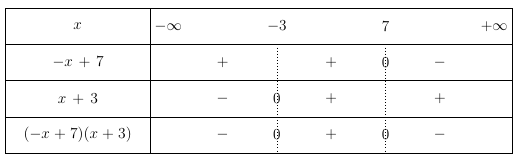
2) $2-3x > 0 \Leftrightarrow -3x > -2 \Leftrightarrow x < \dfrac{2}{3}$
$2-3x = 0 \Leftrightarrow -3x = -2 \Leftrightarrow x = \dfrac{2}{3}$
$5-x > 0 \Leftrightarrow -x > -5 \Leftrightarrow x < 5$
$5-x = 0 \Leftrightarrow -x = -5 \Leftrightarrow x = 5$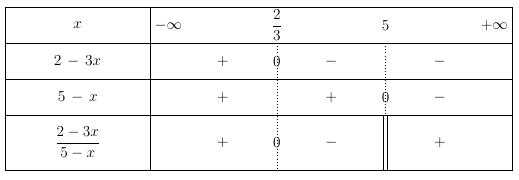
3) $4x-1 > 0 \Leftrightarrow 4x > 1 \Leftrightarrow x > \dfrac{1}{4}$
$4x-1 = 0 \Leftrightarrow 4x = 1 \Leftrightarrow x = \dfrac{1}{4}$
$2-x > 0 \Leftrightarrow -x > -2 \Leftrightarrow x < 2$
$2-x = 0 \Leftrightarrow -x = -2 \Leftrightarrow x = 2$
4) $\dfrac{4x+3}{5x+2}$ $4x+3>0 \Leftrightarrow 4x>-3 \Leftrightarrow x>-\dfrac{3}{4}$
$4x+3=0 \Leftrightarrow 4x=-3 \Leftrightarrow x=-\dfrac{3}{4}$
$5x+2>0\Leftrightarrow 5x>-2 \Leftrightarrow x>-\dfrac{2}{5}$
$5x+2=0\Leftrightarrow 5x=-2 \Leftrightarrow x=-\dfrac{2}{5}$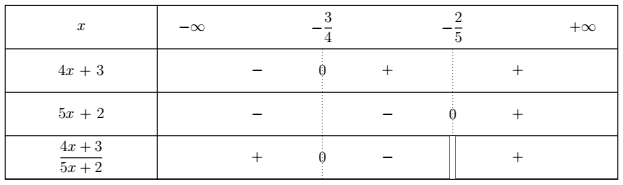
1) $1-x > 0 \Leftrightarrow -x > -1 \Leftrightarrow x < 1$
$1-x = 0 \Leftrightarrow -x = -1 \Leftrightarrow x = 1$
$3 + 2x > 0 \Leftrightarrow 2x > -3 \Leftrightarrow x>- \dfrac{3}{2}$
$3 + 2x = 0 \Leftrightarrow 2x = -3 \Leftrightarrow x=- \dfrac{3}{2}$

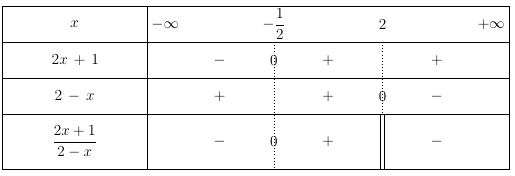
On cherche à résoudre l’inéquation $\dfrac{2x + 1}{2-x} > 0$.
Par conséquent la solution est $\left[-\dfrac{1}{2}; 2\right[$.
1) $x^2 < 1 \Leftrightarrow x^2-1 < 0 \Leftrightarrow (x-1)(x + 1) < 0$.
$x-1 > 0 \Leftrightarrow x > 1$
$x-1 = 0 \Leftrightarrow x = 1$
$x + 1 > 0 \Leftrightarrow x > -1$
$x + 1 = 0 \Leftrightarrow x = -1$
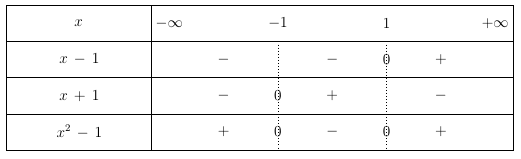
On cherche à résoudre l’inéquation $(x-1)(x + 1) < 0$.
Par conséquent la solution est $[-1;1]$.
2)
$\begin{align} \dfrac{2}{x-2} < \dfrac{3}{x + 1} & \Leftrightarrow \dfrac{2}{x-2}-\dfrac{3}{x + 1} < 0 \\\\ & \Leftrightarrow \dfrac{2(x + 1)}{(x-2)(x + 1)}-\dfrac{3(x-2)}{(x-2)(x + 1)} < 0 \\\\ & \Leftrightarrow \dfrac{2x + 2}{(x-2)(x + 1)}-\dfrac{3x-6}{(x-2)(x + 1)} < 0 \\\\ & \Leftrightarrow \dfrac{-x + 8}{(x-2)(x + 1)} < 0 \end{align}$
$-x + 8 > 0 \Leftrightarrow -x > -8 \Leftrightarrow x < 8$
$-x + 8 = 0 \Leftrightarrow -x = -8 \Leftrightarrow x = 8$
$x-2 > 0 \Leftrightarrow x > 2$
$x-2 = 0 \Leftrightarrow x = 2$
$x + 1 > 0 \Leftrightarrow x > -1$
$x + 1 = 0 \Leftrightarrow x = -1$
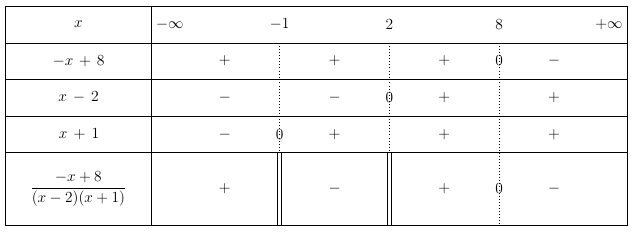
On cherche à résoudre l’inéquation $\dfrac{-x + 8}{(x-2)(x + 1)} < 0$
Par conséquent la solution est $]-1;2[\cup]8;+\infty[$.
3)
$\begin{align}\dfrac{2x + 1}{x + 2} > 3 & \Leftrightarrow \dfrac{2x + 1}{x + 2}-3 > 0 \\\\ & \Leftrightarrow \dfrac{2x + 1}{x + 2}-\dfrac{3(x + 2)}{x + 2} > 0 \\\\ & \Leftrightarrow \dfrac{2x + 1}{x + 2}-\dfrac{3x + 6}{x + 2} > 0 \\\\ & \Leftrightarrow \dfrac{-x-5}{x + 2} > 0 \end{align}$
$-x-5 > 0 \Leftrightarrow -x > 5 \Leftrightarrow x < -5$
$-x-5 = 0 \Leftrightarrow -x > 5 \Leftrightarrow x = -5$
$x + 2 > 0 \Leftrightarrow x > -2$ $x + 2 = 0 \Leftrightarrow x = -2$
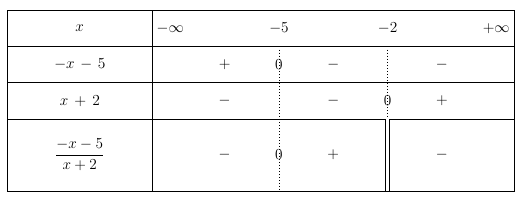
On cherche à résoudre l’inéquation $\dfrac{-x-5}{x + 2} > 0 $
Par conséquent la solution est $[-5;-2[$.
4)
$\begin{align} \dfrac{1}{x} < \dfrac{1}{2x-1} & \Leftrightarrow \dfrac{1}{x}-\dfrac{1}{2x-1} < 0 \\\\ & \Leftrightarrow \dfrac{2x-1}{x(2x-1)}-\dfrac{x}{x(2x-1)} < 0 \\\\ & \Leftrightarrow \dfrac{x-1}{x(2x-1)} < 0 \end{align}$
$x-1 > 0 \Leftrightarrow x > 1$
$x-1 = 0 \Leftrightarrow x = 1$
$2x-1 > 0 \Leftrightarrow 2x > 1 \Leftrightarrow x > \dfrac{1}{2}$
$2x-1 = 0 \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}$
Ne pas oublier de prendre en compte le signe de $x$, dont l’étude est triviale, dans le tableau de signes.

On cherche à résoudre l’inéquation $\dfrac{x-1}{x(2x-1)} < 0$.
Par conséquent la solution est $]-\infty;0[\cup\left]\dfrac{1}{2};1\right[$.
Exercice 1
Dans chacun des cas, fournir les tableaux de signes correspondants.
1) $(2x + 1)(x-3)$
2) $(x-2)(x-5)$
3) $(3x-5)(-2-x)$
4) $(-5x+1)(3-4x)$
5) $(4x+7)(5-3x)$
Correction Exercice 1
Dans chacun des cas, fournir les tableaux de signes correspondants.
1) $(2x + 1)(x-3)$
2) $(x-2)(x-5)$
3) $(3x-5)(-2-x)$
4) $(-5x+1)(3-4x)$
5) $(4x+7)(5-3x)$
1) $2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x =-\dfrac{1}{2}$
$x-3 > 0 \Leftrightarrow x > 3$
$x-3 = 0 \Leftrightarrow x = 3$
2) $x-2> 0 \Leftrightarrow x > 2$
$x-2= 0 \Leftrightarrow x = 2$
$x-5 > 0 \Leftrightarrow x > 5$
$x-5 = 0 \Leftrightarrow x = 5$
3) $3x-5 > 0 \Leftrightarrow 3x > 5 \Leftrightarrow x > \dfrac{5}{3}$
$3x-5 = 0 \Leftrightarrow 3x = 5 \Leftrightarrow x = \dfrac{5}{3}$
$-2-x > 0 \Leftrightarrow -x > 2 \Leftrightarrow x < -2$
$-2-x = 0 \Leftrightarrow -x = 2 \Leftrightarrow x = -2$
4) $-5x+1>0 \Leftrightarrow -5x>-1 \Leftrightarrow x<\dfrac{1}{5}$
$-5x+1=0\Leftrightarrow -5x=-1 \Leftrightarrow x=\dfrac{1}{5}$
$3-4x>0\Leftrightarrow -4x>-3 \Leftrightarrow x<\dfrac{3}{4}$
$3-4x=0 \Leftrightarrow -4x=-3 \Leftrightarrow x=\dfrac{3}{4}$
5) $4x+7>0 \Leftrightarrow 4x>-7 \Leftrightarrow x>-\dfrac{7}{4}$
$4x+7=0 \Leftrightarrow 4x=-7 \Leftrightarrow x=-\dfrac{7}{4}$
$5-3x>0 \Leftrightarrow -3x>-5 \Leftrightarrow x<\dfrac{5}{3}$
$5-3x=0 \Leftrightarrow -3x=-5 \Leftrightarrow x=\dfrac{5}{3}$
Exercice 2
Résoudre les inégalités suivantes :
1) $(3x + 1)(2x + 3) > 0$
2) $(x-3)(4 + x) > 0$
3) $(5-x)(2x + 1) < 0$
4) $(-x +7)(x + 3) > 0$
Correction Exercice 2 Résoudre les inégalités suivantes :
1) $(3x + 1)(2x + 3) > 0$
2) $(x-3)(4 + x) > 0$
3) $(5-x)(2x + 1) < 0$
4) $(-x +7)(x + 3) > 0$
1) $3x + 1 > 0 \Leftrightarrow 3x > -1\Leftrightarrow x > -\dfrac{1}{3}$
$3x + 1 = 0 \Leftrightarrow 3x = -1\Leftrightarrow x = -\dfrac{1}{3}$
$2x + 3 > 0 \Leftrightarrow 2x > -3 \Leftrightarrow x > -\dfrac{3}{2}$
$2x + 3 = 0 \Leftrightarrow 2x = -3 \Leftrightarrow x = -\dfrac{3}{2}$
On cherche à résoudre l’inéquation $(3x + 1)(2x + 3) > 0$.
Par conséquent la solution est $\left]-\infty;-\dfrac{3}{2}\right[\cup\left]-\dfrac{1}{3};+\infty\right[$.
2) $x-3 > 0 \Leftrightarrow x > 3$
$x-3 = 0 \Leftrightarrow x = 3$
$4+x > 0 \Leftrightarrow x > -4$
$4+x = 0 \Leftrightarrow x = -4$
On cherche à résoudre l’inéquation $(x-3)(4 + x) > 0$.
Par conséquent la solution est $]-\infty;-4]\cup[3;+\infty[$.
3) $5-x > 0 \Leftrightarrow -x > -5 \Leftrightarrow x < 5$
$5-x = 0 \Leftrightarrow -x > -5 \Leftrightarrow x = 5$
$2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x = -\dfrac{1}{2}$
$5-x = 0 \Leftrightarrow -x > -5 \Leftrightarrow x = 5$
$2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x = -\dfrac{1}{2}$

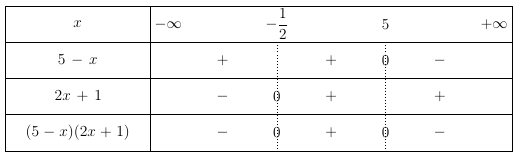
On cherche à résoudre l’inéquation $(5-x)(2x + 1) < 0$.
Par conséquent la solution est $\left]-\infty;-\dfrac{1}{2}\right[\cup]5;+\infty[$.
4) $-x + 7 > 0 \Leftrightarrow -x > -7 \Leftrightarrow x < 7$
$-x + 7 = 0 \Leftrightarrow -x = -7 \Leftrightarrow x = 7$
$x + 3 > 0 \Leftrightarrow x > -3$
$x + 3 = 0 \Leftrightarrow x = -3$
4) $-x + 7 > 0 \Leftrightarrow -x > -7 \Leftrightarrow x < 7$
$-x + 7 = 0 \Leftrightarrow -x = -7 \Leftrightarrow x = 7$
$x + 3 > 0 \Leftrightarrow x > -3$
$x + 3 = 0 \Leftrightarrow x = -3$

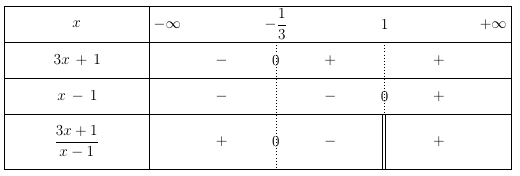
On cherche à résoudre l’inéquation $(-x +7)(x + 3) > 0$.
Par conséquent la solution est $[-3;7]$.
1) $3x + 1 > 0 \Leftrightarrow 3x > -1 \Leftrightarrow x > -\dfrac{1}{3}$
$3x + 1 = 0 \Leftrightarrow 3x = -1 \Leftrightarrow x = -\dfrac{1}{3}$
$x -1 > 0 \Leftrightarrow x > 1$
$x -1 = 0 \Leftrightarrow x = 1$
Par conséquent la solution est $[-3;7]$.
Exercice 3
1) $\dfrac{3x + 1}{x-1}$
2) $\dfrac{2-3x}{5-x}$
3) $\dfrac{4x-1}{2-x}$
4) $\dfrac{4x+3}{5x+2}$
Correction Exercice 3 1) $\dfrac{3x + 1}{x-1}$
2) $\dfrac{2-3x}{5-x}$
3) $\dfrac{4x-1}{2-x}$
4) $\dfrac{4x+3}{5x+2}$
1) $3x + 1 > 0 \Leftrightarrow 3x > -1 \Leftrightarrow x > -\dfrac{1}{3}$
$3x + 1 = 0 \Leftrightarrow 3x = -1 \Leftrightarrow x = -\dfrac{1}{3}$
$x -1 > 0 \Leftrightarrow x > 1$
$x -1 = 0 \Leftrightarrow x = 1$

2) $2-3x > 0 \Leftrightarrow -3x > -2 \Leftrightarrow x < \dfrac{2}{3}$
$2-3x = 0 \Leftrightarrow -3x = -2 \Leftrightarrow x = \dfrac{2}{3}$
$5-x > 0 \Leftrightarrow -x > -5 \Leftrightarrow x < 5$
$5-x = 0 \Leftrightarrow -x = -5 \Leftrightarrow x = 5$

3) $4x-1 > 0 \Leftrightarrow 4x > 1 \Leftrightarrow x > \dfrac{1}{4}$
$4x-1 = 0 \Leftrightarrow 4x = 1 \Leftrightarrow x = \dfrac{1}{4}$
$2-x > 0 \Leftrightarrow -x > -2 \Leftrightarrow x < 2$
$2-x = 0 \Leftrightarrow -x = -2 \Leftrightarrow x = 2$

4) $\dfrac{4x+3}{5x+2}$ $4x+3>0 \Leftrightarrow 4x>-3 \Leftrightarrow x>-\dfrac{3}{4}$
$4x+3=0 \Leftrightarrow 4x=-3 \Leftrightarrow x=-\dfrac{3}{4}$
$5x+2>0\Leftrightarrow 5x>-2 \Leftrightarrow x>-\dfrac{2}{5}$
$5x+2=0\Leftrightarrow 5x=-2 \Leftrightarrow x=-\dfrac{2}{5}$

Exercice 4
Résoudre les inégalités suivantes :
1) $\dfrac{1-x}{3 + 2x} > 0$
2) $\dfrac{5 + 2x}{4x + 1} < 0$
3) $\dfrac{2x + 1}{2-x} > 0$
Correction Exercice 4 Résoudre les inégalités suivantes :
1) $\dfrac{1-x}{3 + 2x} > 0$
2) $\dfrac{5 + 2x}{4x + 1} < 0$
3) $\dfrac{2x + 1}{2-x} > 0$
1) $1-x > 0 \Leftrightarrow -x > -1 \Leftrightarrow x < 1$
$1-x = 0 \Leftrightarrow -x = -1 \Leftrightarrow x = 1$
$3 + 2x > 0 \Leftrightarrow 2x > -3 \Leftrightarrow x>- \dfrac{3}{2}$
$3 + 2x = 0 \Leftrightarrow 2x = -3 \Leftrightarrow x=- \dfrac{3}{2}$

On cherche à résoudre l’inéquation $\dfrac{1-x}{3 + 2x} > 0$.
Par conséquent la solution est $\left]-\dfrac{3}{2};1\right[$
2) $5 + 2x > 0 \Leftrightarrow 2x > -5 \Leftrightarrow x > -\dfrac{5}{2}$
$5 + 2x = 0 \Leftrightarrow 2x = -5 \Leftrightarrow x = -\dfrac{5}{2}$
$4x + 1 > 0 \Leftrightarrow 4x > -1\Leftrightarrow x > -\dfrac{1}{4}$
$4x + 1 = 0 \Leftrightarrow 4x = -1\Leftrightarrow x = -\dfrac{1}{4}$

2) $5 + 2x > 0 \Leftrightarrow 2x > -5 \Leftrightarrow x > -\dfrac{5}{2}$
$5 + 2x = 0 \Leftrightarrow 2x = -5 \Leftrightarrow x = -\dfrac{5}{2}$
$4x + 1 > 0 \Leftrightarrow 4x > -1\Leftrightarrow x > -\dfrac{1}{4}$
$4x + 1 = 0 \Leftrightarrow 4x = -1\Leftrightarrow x = -\dfrac{1}{4}$

On cherche à résoudre l’inéquation $\dfrac{5 + 2x}{4x + 1} < 0$.
Par conséquent la solution est $\left[-\dfrac{5}{2};-\dfrac{1}{4}\right[$.
3) $2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x = -\dfrac{1}{2}$
$2-x > 0 \Leftrightarrow -x > -2 \Leftrightarrow x
$2-x = 0 \Leftrightarrow -x = -2 \Leftrightarrow x =2$
Par conséquent la solution est $\left[-\dfrac{5}{2};-\dfrac{1}{4}\right[$.
3) $2x + 1 > 0 \Leftrightarrow 2x > -1 \Leftrightarrow x > -\dfrac{1}{2}$
$2x + 1 = 0 \Leftrightarrow 2x = -1 \Leftrightarrow x = -\dfrac{1}{2}$
$2-x > 0 \Leftrightarrow -x > -2 \Leftrightarrow x
$2-x = 0 \Leftrightarrow -x = -2 \Leftrightarrow x =2$

On cherche à résoudre l’inéquation $\dfrac{2x + 1}{2-x} > 0$.
Par conséquent la solution est $\left[-\dfrac{1}{2}; 2\right[$.
Exercice 5
Résoudre les inégalités suivantes :
1) $x^2 < 1$
2) $\dfrac{2}{x-2} < \dfrac{3}{x + 1}$
3) $\dfrac{2x + 1}{x + 2} > 3$
4) $\dfrac{1}{x} < \dfrac{1}{2x-1}$
Correction Exercice 5 Résoudre les inégalités suivantes :
1) $x^2 < 1$
2) $\dfrac{2}{x-2} < \dfrac{3}{x + 1}$
3) $\dfrac{2x + 1}{x + 2} > 3$
4) $\dfrac{1}{x} < \dfrac{1}{2x-1}$
1) $x^2 < 1 \Leftrightarrow x^2-1 < 0 \Leftrightarrow (x-1)(x + 1) < 0$.
$x-1 > 0 \Leftrightarrow x > 1$
$x-1 = 0 \Leftrightarrow x = 1$
$x + 1 > 0 \Leftrightarrow x > -1$
$x + 1 = 0 \Leftrightarrow x = -1$

On cherche à résoudre l’inéquation $(x-1)(x + 1) < 0$.
Par conséquent la solution est $[-1;1]$.
2)
$\begin{align} \dfrac{2}{x-2} < \dfrac{3}{x + 1} & \Leftrightarrow \dfrac{2}{x-2}-\dfrac{3}{x + 1} < 0 \\\\ & \Leftrightarrow \dfrac{2(x + 1)}{(x-2)(x + 1)}-\dfrac{3(x-2)}{(x-2)(x + 1)} < 0 \\\\ & \Leftrightarrow \dfrac{2x + 2}{(x-2)(x + 1)}-\dfrac{3x-6}{(x-2)(x + 1)} < 0 \\\\ & \Leftrightarrow \dfrac{-x + 8}{(x-2)(x + 1)} < 0 \end{align}$
$-x + 8 > 0 \Leftrightarrow -x > -8 \Leftrightarrow x < 8$
$-x + 8 = 0 \Leftrightarrow -x = -8 \Leftrightarrow x = 8$
$x-2 > 0 \Leftrightarrow x > 2$
$x-2 = 0 \Leftrightarrow x = 2$
$x + 1 > 0 \Leftrightarrow x > -1$
$x + 1 = 0 \Leftrightarrow x = -1$

On cherche à résoudre l’inéquation $\dfrac{-x + 8}{(x-2)(x + 1)} < 0$
Par conséquent la solution est $]-1;2[\cup]8;+\infty[$.
3)
$\begin{align}\dfrac{2x + 1}{x + 2} > 3 & \Leftrightarrow \dfrac{2x + 1}{x + 2}-3 > 0 \\\\ & \Leftrightarrow \dfrac{2x + 1}{x + 2}-\dfrac{3(x + 2)}{x + 2} > 0 \\\\ & \Leftrightarrow \dfrac{2x + 1}{x + 2}-\dfrac{3x + 6}{x + 2} > 0 \\\\ & \Leftrightarrow \dfrac{-x-5}{x + 2} > 0 \end{align}$
$-x-5 > 0 \Leftrightarrow -x > 5 \Leftrightarrow x < -5$
$-x-5 = 0 \Leftrightarrow -x > 5 \Leftrightarrow x = -5$
$x + 2 > 0 \Leftrightarrow x > -2$ $x + 2 = 0 \Leftrightarrow x = -2$

On cherche à résoudre l’inéquation $\dfrac{-x-5}{x + 2} > 0 $
Par conséquent la solution est $[-5;-2[$.
4)
$\begin{align} \dfrac{1}{x} < \dfrac{1}{2x-1} & \Leftrightarrow \dfrac{1}{x}-\dfrac{1}{2x-1} < 0 \\\\ & \Leftrightarrow \dfrac{2x-1}{x(2x-1)}-\dfrac{x}{x(2x-1)} < 0 \\\\ & \Leftrightarrow \dfrac{x-1}{x(2x-1)} < 0 \end{align}$
$x-1 > 0 \Leftrightarrow x > 1$
$x-1 = 0 \Leftrightarrow x = 1$
$2x-1 > 0 \Leftrightarrow 2x > 1 \Leftrightarrow x > \dfrac{1}{2}$
$2x-1 = 0 \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}$
Ne pas oublier de prendre en compte le signe de $x$, dont l’étude est triviale, dans le tableau de signes.

On cherche à résoudre l’inéquation $\dfrac{x-1}{x(2x-1)} < 0$.
Par conséquent la solution est $]-\infty;0[\cup\left]\dfrac{1}{2};1\right[$.







Commentaires
Enregistrer un commentaire